已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
如果弧长为6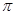 的弧所对的圆心角为60°,那么这条弧所在的圆的半径是( )
的弧所对的圆心角为60°,那么这条弧所在的圆的半径是( )
| A.18 | B.12 | C.36 | D.6 |
如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若BD= ,则∠ACD= 度.
,则∠ACD= 度.

如图,圆锥的底面半径OB=6cm,高OC=8cm.则这个圆锥的侧面积是( )

| A.30cm2 | B.30πcm2 | C.60πcm2 | D.120cm2 |
△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是( )
| A.80° | B.160° | C.100° | D.80°或100° |
如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则 的长为( )
的长为( )
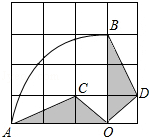
| A.π | B.6π | C.3π | D.1.5π |
已知⊙O的半径为5,圆心O到直线l的距离为3,则反映直线l与⊙O的位置关系的图形是( )
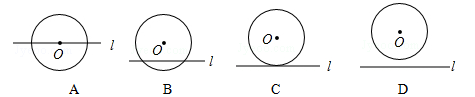
试题篮
()