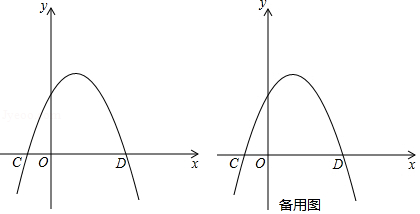
已知抛物线 ,其中 ,且 .
(1) 直接写出关于 的一元二次方程 的一个根;
(2) 证明: 抛物线 的顶点 在第三象限;
(3) 直线 与 , 轴分别相交于 , 两点, 与抛物线 相交于 , 两点 . 设抛物线 的对称轴与 轴相交于 . 如果在对称轴左侧的抛物线上存在点 ,使得 与 相似, 并且 ,求此时抛物线的表达式 .
某市总预算 亿元用三年时间建成一条轨道交通线.轨道交通线由线路敷设、搬迁安置、辅助配套三项工程组成.从2015年开始,市政府在每年年初分别对三项工程进行不同数额的投资.
2015年年初,对线路敷设、搬迁安置的投资分别是辅助配套投资的2倍、4倍.随后两年,线路敷设投资每年都增加 亿元,预计线路敷设三年总投资为54亿元时会顺利如期完工;搬迁安置投资从2016年年初开始逐年按同一百分数递减,依此规律,在2017年年初只需投资5亿元,即可顺利如期完工;辅助配套工程在2016年年初的投资在前一年基础上的增长率是线路敷设2016年投资增长率的1.5倍,2017年年初的投资比该项工程前两年投资的总和还多4亿元,若这样,辅助配套工程也可以如期完工.经测算,这三年的线路敷设、辅助配套工程的总投资资金之比达到 .
(1)这三年用于辅助配套的投资将达到多少亿元?
(2)市政府2015年年初对三项工程的总投资是多少亿元?
(3)求搬迁安置投资逐年递减的百分数.
阅读:能够成为直角三角形三条边长的三个正整数 , , ,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为: 其中 , , 是互质的奇数.
应用:当 时,求有一边长为5的直角三角形的另外两条边长.
“和谐号”火车从车站出发,在行驶过程中速度 (单位: 与时间 (单位: 的关系如图所示,其中线段 轴.
请根据图象提供的信息解答下列问题:
(1)当 ,求 关于 的函数解析式;
(2)求 点的坐标.

市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够,导致出现需要租用却未租到车的现象,现将随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
时间 |
第一天 |
第二天 |
第三天 |
第四天 |
第五天 |
需要租用自行车却未租到车的人数(人 |
1500 |
1200 |
1300 |
1300 |
1200 |
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在 需要租用公共自行车的人数是多少?
在平面直角坐标系 中,规定:抛物线 的伴随直线为 .例如:抛物线 的伴随直线为 ,即 .
(1)在上面规定下,抛物线 的顶点坐标为 ,伴随直线为 ,抛物线 与其伴随直线的交点坐标为 和 ;
(2)如图,顶点在第一象限的抛物线 与其伴随直线相交于点 , (点 在点 的左侧),与 轴交于点 , .
①若 ,求 的值;
②如果点 是直线 上方抛物线上的一个动点, 的面积记为 ,当 取得最大值 时,求 的值.
为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有 , 两种型号的健身器材可供选择.
(1)劲松公司2015年每套 型健身器材的售价为2.5万元,经过连续两年降价,2017年每套售价为1.6万元,求每套 型健身器材年平均下降率 ;
(2)2017年市政府经过招标,决定年内采购并安装劲松公司 , 两种型号的健身器材共80套,采购专项经费总计不超过112万元,采购合同规定:每套 型健身器材售价为1.6万元,每套 型健身器材售价为 万元.
① 型健身器材最多可购买多少套?
②安装完成后,若每套 型和 型健身器材一年的养护费分别是购买价的 和 ,市政府计划支出10万元进行养护,问该计划支出能否满足一年的养护需要?
已知关于 的一元二次方程 有两个实数根 , .
(1)求 的取值范围;
(2)若 , 满足 ,求 的值.
如图,矩形 的两边在坐标轴上,点 的坐标为 ,抛物线 过点 , 两点,且与 轴的一个交点为 ,点 是线段 上的动点,设 .
(1)请直接写出 、 两点的坐标及抛物线的解析式;
(2)过点 作 ,交抛物线于点 ,连接 ,当 为何值时, ?
(3)点 是 轴上的动点,过点 作 ,交 于点 ,作 ,交 于点 ,当四边形 为正方形时,请求出 的值.

如图,在 中, , 是中线, ,一个以点 为顶点的 角绕点 旋转,使角的两边分别与 、 的延长线相交,交点分别为点 , , 与 交于点 , 与 交于点 .

(1)如图1,若 ,求证: ;
(2)如图2,在 绕点 旋转的过程中:
①探究三条线段 , , 之间的数量关系,并说明理由;
②若 , ,求 的长.
为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为 的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为 ,种草所需费用 (元)与 的函数关系式为 ,其图象如图所示:栽花所需费用 (元 与 的函数关系式为 .
(1)请直接写出 、 和 的值;
(2)设这块 空地的绿化总费用为 (元),请利用 与 的函数关系式,求出绿化总费用 的最大值;
(3)若种草部分的面积不少于 ,栽花部分的面积不少于 ,请求出绿化总费用 的最小值.

试题篮
()