初中数学计算题

金桥学校“科技体艺节”期间，八年级数学活动小组的任务是测量学校旗杆 $\mathit{AB}$的高，他们在旗杆正前方台阶上的点 $C$处，测得旗杆顶端 $A$的仰角为 $45°$，朝着旗杆的方向走到台阶下的点 $F$处，测得旗杆顶端 $A$的仰角为 $60°$，已知升旗台的高度 $\mathit{BE}$为1米，点 $C$距地面的高度 $\mathit{CD}$为3米，台阶 $\mathit{CF}$的坡角为 $30°$，且点 $E$、 $F$、 $D$在同一条直线上，求旗杆 $\mathit{AB}$的高度（计算结果精确到0.1米，参考数据： $\sqrt{2}\approx 1.41$， $\sqrt{3}\approx 1.73)$

已知：如图，在 $\text{Rt}\Delta \text{ACB}$中， $\angle \mathit{ACB}=90°$，点 $D$是 $\mathit{AB}$的中点，且 $\mathit{CD}=\frac{1}{2}\mathit{AB}$，点 $E$是 $\mathit{CD}$的中点，过点 $C$作 $\mathit{CF}//\mathit{AB}$交 $\mathit{AE}$的延长线于点 $F$．

（1）求证： $\mathit{\Delta ADE}\cong \mathit{\Delta FCE}$；

（2）若 $\angle \mathit{DCF}=120°$， $\mathit{DE}=2$，求 $\mathit{BC}$的长．

先化简，再求值： ${(2x+1)}^2-2(x-1)(x+3)-2$，其中 $x=\sqrt{2}$．

小明同学在一次社会实践活动中，通过对某种蔬菜在1月份至7月份的市场行情进行统计分析后得出如下规律：

①该蔬菜的销售单价 $P$（单位：元 $/$千克）与时间 $x$（单位：月份）满足关系： $P=9-x$；

②该蔬菜的平均成本 $y$（单位：元 $/$千克）与时间 $x$（单位：月份）满足二次函数关系 $y=a{x}^2+\mathit{bx}+10$．

已知4月份的平均成本为2元 $/$千克，6月份的平均成本为1元 $/$千克．

（1）求该二次函数的解析式；

（2）请运用小明统计的结论，求出该蔬菜在第几月份的平均利润 $L$（单位：元 $/$千克）最大？最大平均利润是多少？（注：平均利润 $=$销售单价 $-$平均成本）

随着社会的发展，私家车变得越来越普及，使用节能低油耗汽车，对环保有着非常积极的意义，某市有关部门对本市的某一型号的若干辆汽车，进行了一项油耗抽样实验：即在同一条件下，被抽样的该型号汽车，在油耗 $1L$的情况下，所行驶的路程（单位： $\mathit{km})$进行统计分析，结果如图所示：

（注：记 $A$为 $12~12.5$， $B$为 $12.5~13$， $C$为 $13~13.5$， $D$为 $13.5~14$， $E$为 $14~14.5)$

请依据统计结果回答以下问题：

（1）试求进行该试验的车辆数；

（2）请补全频数分布直方图；

（3）若该市有这种型号的汽车约900辆（不考虑其他因素），请利用上述统计数据初步预测，该市约有多少辆该型号的汽车，在耗油 $1L$的情况下可以行驶 $13\mathit{km}$以上？

已知关于 $x$的一元二次方程 $x^2-4x-m^2=0$

（1）求证：该方程有两个不等的实根；

（2）若该方程的两实根 $x_1$、 $x_2$满足 $x_1+2x_2=9$，求 $m$的值．

已知关于 $x$的不等式组 $\left\{\begin{array}{c}5x+1>3(x-1)\\ \frac{1}{2}x⩽8-\frac{3}{2}x+2a\end{array}\right.$恰好有两个整数解，求实数 $a$的取值范围．

先化简，再求值： $(\frac{2}{a-1}-\frac{2a+1}{a^2-1})÷\frac{1}{a-1}$，其中 $a=2\sin 60°-\tan 45°$．

计算： ${(-2)}^3+\sqrt{16}+1^0+|-3+\sqrt{3}|$．

已知：如图所示，在平面直角坐标系 $\mathit{xOy}$中，四边形 $\mathit{OABC}$是矩形， $\mathit{OA}=4$， $\mathit{OC}=3$，动点 $P$从点 $C$出发，沿射线 $\mathit{CB}$方向以每秒2个单位长度的速度运动；同时，动点 $Q$从点 $O$出发，沿 $x$轴正半轴方向以每秒1个单位长度的速度运动．设点 $P$、点 $Q$的运动时间为 $t\left(s\right)$．

（1）当 $t=1s$时，求经过点 $O$， $P$， $A$三点的抛物线的解析式；

（2）当 $t=2s$时，求 $\tan \angle \mathit{QPA}$的值；

（3）当线段 $\mathit{PQ}$与线段 $\mathit{AB}$相交于点 $M$，且 $\mathit{BM}=2\mathit{AM}$时，求 $t\left(s\right)$的值；

（4）连接 $\mathit{CQ}$，当点 $P$， $Q$在运动过程中，记 $\mathit{\Delta CQP}$与矩形 $\mathit{OABC}$重叠部分的面积为 $S$，求 $S$与 $t$的函数关系式．

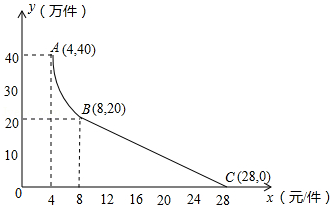
某电子科技有限公司用160万元，作为新产品的研发费用，成功研制出了一种市场急需的电子产品，已于当年投入生产并进行销售．已知生产这种电子产品的成本为4元 $/$件，在销售过程中发现：每年的年销售量 $y$（万件）与销售价格 $x$（元 $/$件）的关系如图所示，其中 $\mathit{AB}$为反比例函数图象的一部分， $\mathit{BC}$为一次函数图象的一部分．设公司销售这种电子产品的年利润为 $s$（万元）．（注：若上一年盈利，则盈利不计入下一年的年利润；若上一年亏损，则亏损计作下一年的成本． $)$

（1）请求出 $y$（万件）与 $x$（元 $/$件）之间的函数关系式；

（2）求出第一年这种电子产品的年利润 $s$（万元）与 $x$（元 $/$件）之间的函数关系式，并求出第一年年利润的最大值．

（3）假设公司的这种电子产品第一年恰好按年利润 $s$（万元）取得最大值时进行销售，现根据第一年的盈亏情况，决定第二年将这种电子产品每件的销售价格 $x$（元 $)$定在8元以上 $(x>8)$，当第二年的年利润不低于103万元时，请结合年利润 $s$（万元）与销售价格 $x$（元 $/$件）的函数示意图，求销售价格 $x$（元 $/$件）的取值范围．

在黄冈长江大桥的东端一处空地上，有一块矩形的标语牌 $\mathit{ABCD}$（如图所示），已知标语牌的高 $\mathit{AB}=5m$，在地面的点 $E$处，测得标语牌点 $A$的仰角为 $30°$，在地面的点 $F$处，测得标语牌点 $A$的仰角为 $75°$，且点 $E$， $F$， $B$， $C$在同一直线上，求点 $E$与点 $F$之间的距离．（计算结果精确到0.1米，参考数据： $\sqrt{2}\approx 1.41$， $\sqrt{3}\approx 1.73)$

已知：如图，一次函数 $y=-2x+1$与反比例函数 $y=\frac{k}{x}$的图象有两个交点 $A(-1,m)$和 $B$，过点 $A$作 $\mathit{AE}\perp x$轴，垂足为点 $E$；过点 $B$作 $\mathit{BD}\perp y$轴，垂足为点 $D$，且点 $D$的坐标为 $(0,-2)$，连接 $\mathit{DE}$．

（1）求 $k$的值；

（2）求四边形 $\mathit{AEDB}$的面积．

黄麻中学为了创建全省“最美书屋”，购买了一批图书，其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元，已知学校用12000元购买的科普类图书的本数与用9000元购买的文学类图书的本数相等，求学校购买的科普类图书和文学类图书平均每本的价格各是多少元？

已知关于 $x$的一元二次方程 $x^2+(2k+1)x+k^2=0$①有两个不相等的实数根．

（1）求 $k$的取值范围；

（2）设方程①的两个实数根分别为 $x_1$， $x_2$，当 $k=1$时，求 $x_1^2+x_2^2$的值．