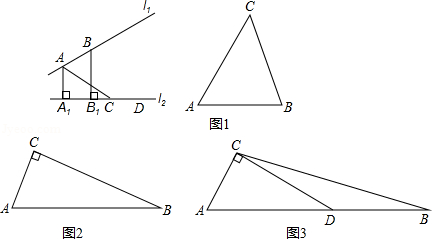
如图,平面内的两条直线 、 ,点 , 在直线 上,点 、 在直线 上,过 、 两点分别作直线 的垂线,垂足分别为 , ,我们把线段 叫做线段 在直线 上的正投影,其长度可记作 或 ,特别地线段 在直线 上的正投影就是线段 .
请依据上述定义解决如下问题:
(1)如图1,在锐角 中, , ,则 ;
(2)如图2,在 中, , , ,求 的面积;
(3)如图3,在钝角 中, ,点 在 边上, , , ,求 ,
如图, 是 的弦,过点 作 , 交 于 , .
(1)求证: 是 的切线;
(2)已知 ,点 是 上的一点.
①求 的度数;
②若 ,求 的长.

“绿水青山就是金山银山”为了更进一步优化环境,甲、乙两队承担河道整治任务.甲、乙两个工程队每天共整治河道1500米,且甲整治3600米河道用的时间与乙工程队整治2400米所用的时间相等.求甲工程队每天修多少米?
如图所示,二次函数 的图象与一次函数 的图象交于 、 两点,点 在点 的右侧,直线 分别与 、 轴交于 、 两点,其中 .
(1)求 、 两点的横坐标;
(2)若 是以 为腰的等腰三角形,求 的值;
(3)二次函数图象的对称轴与 轴交于点 ,是否存在实数 ,使得 ,若存在,求出 的值;若不存在,说明理由.

(生活观察)甲、乙两人买菜,甲习惯买一定质量的菜,乙习惯买一定金额的菜,两人每次买菜的单价相同,例如:
第一次:
菜价3元 千克 |
||
质量 |
金额 |
|
甲 |
1千克 |
3元 |
乙 |
1千克 |
3元 |
第二次:
菜价2元 千克 |
||
质量 |
金额 |
|
甲 |
1千克 |
元 |
乙 |
千克 |
3元 |
(1)完成上表;
(2)计算甲两次买菜的均价和乙两次买菜的均价.(均价 总金额 总质量)
(数学思考)设甲每次买质量为 千克的菜,乙每次买金额为 元的菜,两次的单价分别是 元 千克、 元 千克,用含有 、 、 、 的式子,分别表示出甲、乙两次买菜的均价 、 ,比较 、 的大小,并说明理由.
(知识迁移)某船在相距为 的甲、乙两码头间往返航行一次.在没有水流时,船的速度为 ,所需时间为 ;如果水流速度为 时 ,船顺水航行速度为 ,逆水航行速度为 ,所需时间为 .请借鉴上面的研究经验,比较 、 的大小,并说明理由.
体育器材室有 、 两种型号的实心球,1只 型球与1只 型球的质量共7千克,3只 型球与1只 型球的质量共13千克.
(1)每只 型球、 型球的质量分别是多少千克?
(2)现有 型球、 型球的质量共17千克,则 型球、 型球各有多少只?
在一个不透明的布袋中,有2个红球,1个白球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出1个球,摸到红球的概率是 .
(2)搅匀后先从中任意摸出1个球(不放回),再从余下的球中任意摸出1个球.求两次都摸到红球的概率.(用树状图或表格列出所有等可能出现的结果)
如图,一次函数 的图象交 轴于点 ,与反比例函数 的图象交于点 .
(1)求反比例函数的表达式;
(2)求 的面积.

试题篮
()