初中数学计算题

某校计划采购凳子，商场有 $A$、 $B$两种型号的凳子出售，并规定：对于 $A$型凳子，采购数量若超过250张，则超出部分可在原价基础上每张优惠 $a$元； $B$型凳子的售价为40元 $/$张．学校经测算，若购买300张 $A$型凳子需要花费14250元；若购买500张 $A$型凳子需要花费21250元．

（1）求 $a$的值；

（2）学校要采购 $A$、 $B$两种型号凳子共900张，且购买 $A$型凳子不少于150张且不超过 $B$型凳子数量的2倍，请通过计算帮学校决策如何分配购买数量可以使得总采购费用最少？最少是多少元？

某校为了了解七年级学生“校本课程”的选修情况，在该校七年级学生中随机抽取部分学生进行了问卷调查，问卷设置了“文学欣赏”、“球类运动”、“动漫制作”、“其他”四个选项，每名同学仅选一项，根据调查结果绘制了如下不完整的频数分布表和扇形统计图．

各类“校本课程”选修情况频数分布表

课程类别	频数
文学欣赏	16
球类运动	20
动漫制作	6
其他	$a$
合计	$b$

（1）直接写出 $a$、 $b$、 $m$的值；

（2）若该校七年级共有学生600人，请估计选修“球类运动”的学生人数．

（1）解方程： $2x^2-x-5=0$；

（2）解不等式组： $\left\{\begin{array}{c}3(x+1)>x-1\\ \frac{x+6}{2}⩾2x\end{array}\right.$．

计算：

（1） $\sqrt{3}\times \sqrt{6}-\sqrt{8}+\sqrt{12}$；

（2） ${(x+y)}^2-x(x+y)$．

已知一次函数 $y_1=\mathit{kx}+n(n<0)$和反比例函数 $y_2=\frac{m}{x}(m>0,x>0)$．

（1）如图1，若 $n=-2$，且函数 $y_1$、 $y_2$的图象都经过点 $A(3,4)$．

①求 $m$， $k$的值；

②直接写出当 $y_1>y_2$时 $x$的范围；

（2）如图2，过点 $P(1,0)$作 $y$轴的平行线 $l$与函数 $y_2$的图象相交于点 $B$，与反比例函数 $y_3=\frac{n}{x}(x>0)$的图象相交于点 $C$．

①若 $k=2$，直线 $l$与函数 $y_1$的图象相交点 $D$．当点 $B$、 $C$、 $D$中的一点到另外两点的距离相等时，求 $m-n$的值；

②过点 $B$作 $x$轴的平行线与函数 $y_1$的图象相交于点 $E$．当 $m-n$的值取不大于1的任意实数时，点 $B$、 $C$间的距离与点 $B$、 $E$间的距离之和 $d$始终是一个定值．求此时 $k$的值及定值 $d$．

小李经营一家水果店，某日到水果批发市场批发一种水果．经了解，一次性批发这种水果不得少于 $100\mathit{kg}$，超过 $300\mathit{kg}$时，所有这种水果的批发单价均为3元 $/\mathit{kg}$．图中折线表示批发单价 $y$（元 $/\mathit{kg})$与质量 $x\left(\mathit{kg}\right)$的函数关系．

（1）求图中线段 $\mathit{AB}$所在直线的函数表达式；

（2）小李用800元一次可以批发这种水果的质量是多少？

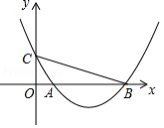
如图，在平面直角坐标系 $\mathit{xOy}$中，二次函数图象的顶点坐标为 $(4,-3)$，该图象与 $x$轴相交于点 $A$、 $B$，与 $y$轴相交于点 $C$，其中点 $A$的横坐标为1．

（1）求该二次函数的表达式；

（2）求 $\tan \angle \mathit{ABC}$．

某体育看台侧面的示意图如图所示，观众区 $\mathit{AC}$的坡度 $i$为 $1:2$，顶端 $C$离水平地面 $\mathit{AB}$的高度为 $10m$，从顶棚的 $D$处看 $E$处的仰角 $\alpha =18°30\text{'}$，竖直的立杆上 $C$、 $D$两点间的距离为 $4m$， $E$处到观众区底端 $A$处的水平距离 $\mathit{AF}$为 $3m$．求：

（1）观众区的水平宽度 $\mathit{AB}$；

（2）顶棚的 $E$处离地面的高度 $\mathit{EF}$． $(\sin 18°30\text{'}\approx 0.32$， $\tan l8°30\text{'}\approx 0.33$，结果精确到 $0.1m)$

小明代表学校参加“我和我的祖国”主题宣传教育活动．该活动分为两个阶段，第一阶段有“歌曲演唱”、“书法展示”、“器乐独奏”3个项目（依次用 $A$、 $B$、 $C$表示），第二阶段有“故事演讲”、“诗歌朗诵”2个项目（依次用 $D$、 $E$表示），参加人员在每个阶段各随机抽取一个项目完成．用画树状图或列表的方法列出小明参加项目的所有等可能的结果，并求小明恰好抽中 $B$、 $D$两个项目的概率．

（1）计算： $(\sqrt{8}-\sqrt{\frac{1}{2}})\times \sqrt{6}$；

（2）解方程： $\frac{2x-5}{x-2}+3=\frac{3x-3}{x-2}$．

如图，抛物线 $y=x^2+\mathit{bx}+c$交 $x$轴于 $A$、 $B$两点，其中点 $A$坐标为 $(1,0)$，与 $y$轴交于点 $C(0,-3)$．

（1）求抛物线的函数表达式；

（2）如图①，连接 $\mathit{AC}$，点 $P$在抛物线上，且满足 $\angle \mathit{PAB}=2\angle \mathit{ACO}$．求点 $P$的坐标；

（3）如图②，点 $Q$为 $x$轴下方抛物线上任意一点，点 $D$是抛物线对称轴与 $x$轴的交点，直线 $\mathit{AQ}$、 $\mathit{BQ}$分别交抛物线的对称轴于点 $M$、 $N$．请问 $\mathit{DM}+\mathit{DN}$是否为定值？如果是，请求出这个定值；如果不是，请说明理由．

超市销售某种儿童玩具，如果每件利润为40元（市场管理部门规定，该种玩具每件利润不能超过60元），每天可售出50件．根据市场调查发现，销售单价每增加2元，每天销售量会减少1件．设销售单价增加 $x$元，每天售出 $y$件．

（1）请写出 $y$与 $x$之间的函数表达式；

（2）当 $x$为多少时，超市每天销售这种玩具可获利润2250元？

（3）设超市每天销售这种玩具可获利 $w$元，当 $x$为多少时 $w$最大，最大值是多少？

宿迁市政府为了方便市民绿色出行，推出了共享单车服务．图①是某品牌共享单车放在水平地面上的实物图，图②是其示意图，其中 $\mathit{AB}$、 $\mathit{CD}$都与地面 $l$平行，车轮半径为 $32\mathit{cm}$， $\angle \mathit{BCD}=64°$， $\mathit{BC}=60\mathit{cm}$，坐垫 $E$与点 $B$的距离 $\mathit{BE}$为 $15\mathit{cm}$．

（1）求坐垫 $E$到地面的距离；

（2）根据经验，当坐垫 $E$到 $\mathit{CD}$的距离调整为人体腿长的0.8时，坐骑比较舒适．小明的腿长约为 $80\mathit{cm}$，现将坐垫 $E$调整至坐骑舒适高度位置 $E^{\text{'}}$，求 $\mathit{EE}\text{'}$的长．

（结果精确到 $0.1\mathit{cm}$，参考数据： $\sin 64°\approx 0.90$， $\cos 64°\approx 0.44$， $\tan 64°\approx 2.05)$

如图，一次函数 $y=\mathit{kx}+b$的图象与反比例函数 $y=-\frac{5}{x}$的图象相交于点 $A(-1,m)$、 $B(n,-1)$两点．

（1）求一次函数表达式；

（2）求 $\mathit{\Delta AOB}$的面积．

先化简，再求值： $(1+\frac{1}{a-1})÷\frac{2a}{a^2-1}$，其中 $a=-2$．