初中数学解答题

已知关于x的方程（k﹣1）x²﹣（k﹣1）x +=0有两个相等的实数根，求k的值．

解方程（1）（x - 3）²＋4x（x - 3）＝0      
（2）x² - 6x - 2=0．

已知函数y=（m²﹣m）x²+（m﹣1）x+m+1．
（1）若这个函数是一次函数，求m的值；
（2）若这个函数是二次函数，则m的值应怎样？

已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D（如图）

（1）求证：AC=BD
（2）若大圆的半径R=10，小圆半径r=8，且圆心O到直线AB的距离为6，求AC的长．

王先生到市行政中心大楼办事，假定乘电梯向上一楼记作+1，向下一楼记-1，王先生从1楼出发，电梯上下楼层依次记录如下（单位：层）：  +6，－3，+10，－8，+12，－7，－10．
（1）请你通过计算说明王先生最后是否回到出发点1楼．
（2）该中心大楼每层高3 m，电梯每向上或下1 m需要耗电0．2度，根据王先生现在所处位置，请你算算，他办事时电梯需要耗电多少度?（本题6分）

把下列各数填入表示它所在的数集的大括号：
－2．4，3，2．008，－，0．1010010001…，－，0，－（－2．28），，－|－4|
无理数集合：{                                  …}；
分数集合：  {                                  …}；
非正整数集合：{                                …}；
正数集合：{                                    …}．

实数a，b，c在数轴上的对应关系如图，化简下面的式子

|a-b|-|c-a|+|b-c|-|a|

如图，在平面直角坐标系中，已知OA=12cm，OB=6cm，点P从O点开始沿OA边向点A以1cm/s的速度移动，点Q从点B开始沿BO边向点O以1cm/s的速度移动，如果P、Q同时出发，用t（单位：秒）表示移动的时间（0≤t≤6），那么：

（1）当t为何值时，△POQ与△AOB相似？
（2）设△POQ的面积为y，求y关于t的函数关系式．

已知关于的一元二次方程有两个实数根和．
（1）求实数的取值范围；
（2）当时，求的值．

小明和小芳做配紫色游戏，如图是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形，并涂上图中所示的颜色．同时转动两个转盘，如果转盘A转出了红色，转盘B转出了蓝色，或者转盘A转出了蓝色，转盘B转出了红色，则红色和蓝色在一起配成紫色．
（1）利用列表或树状图的方法表示此游戏所有可能出现的结果；
（2）若出现紫色，则小明胜，否则小芳胜．此游戏的规则对小明、小芳公平吗？试说明理由．

解方程：
（1）                      
（2）

如图，半圆O直径DE=12，Rt△ABC中，BC=12，∠ACB=90°，∠ABC=30°．半圆O从左到右运动，在运动过程中，点D，E始终在直线BC上，半圆O在△ABC的左侧．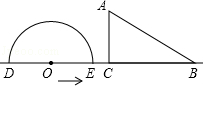

（1）当△ABC的一边与半圆O相切时，请画出符合题意得图形。
（2）当△ABC的一边与半圆O相切时，如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分，求重叠部分的面积

如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．

（1）请完成如下操作：①以点O为原点、竖直和水平方向为轴、网格边长为单位长，建立平面直角坐标系；②根据图形提供的信息，标出该圆弧所在圆的圆心D，并连接AD、CD．
（2）请在（1）的基础上，完成下列填空：
①写出点的坐标：C      、D       ；
②⊙D的半径=     （结果保留根号）；
③∠ADC的度数为    ．
④网格图中是否存在过点B的直线BE是⊙D的切线，如果没有，请说明理由；如果有，请直接写出直线BE的函数解析式。

如图，以点P（﹣1，0）为圆心的圆，交x轴于B、C两点（B在C的左侧），交y轴于A、D两点（A在D的下方），AD=，其中∠BAC=90°，将△ABC绕点P旋转180°，得到△MCB．

（1）求B、C两点的坐标；
（2）请在图中画出线段MB、MC，并判断四边形ACMB的形状（不必证明），求出点M的坐标；
（3）动直线l从与BM重合的位置开始绕点B顺时针旋转，到与BC重合时停止，设直线l与CM交点为E，点Q为BE的中点，过点E作EG⊥BC于G，连接MQ、QG．请问在旋转过程中∠MQG的大小是否变化？若不变，求出∠MQG的度数；若变化，请说明理由．

在平面直角坐标系中，抛物线C₁:y=ax²－1
（1）若抛物线过点A（1,0），求抛物线C₁的解析式；
（2）将（1）中的抛物线C₁平移，使其顶点在直线L₁：y=x上，得到抛物线C₂，若直线L₁与抛物线C₂交于点C、D，求线段CD的长；
（3）将（1）中的抛物线C₁绕点A旋转180⁰后得到抛物线C₃，直线y=kx－2k＋4与抛物线C₃只有唯一交点，求符合条件的直线l的解析式。