初中数学解答题

（本题10分）如图13－1，为美化校园环境，某校计划在一块长为60米，宽为40米的长方形空地上修建一个长方形花圃，并将花圃四周余下的空地修建成同样宽的通道，设通道宽为米．
（1）用含的式子表示花圃的面积；
（2）如果通道所占面积是整个长方形空地面积的，求出此时通道的宽；
（3）若按上述要求施工，同时校长希望长方形花圃的形状与原长方形空地的形状相似，聪明的你想一想能不能满足校长的要求，若能，求出此时通道的宽；若不能，则说明理由。

当a=3，b=﹣1时
（1）求代数式a²﹣b²和（a+b）（a﹣b）的值；
（2）猜想这两个代数式的值有何关系？
（3）根据（1）（2），你能用简便方法算出a=2008，b=2007时，a²﹣b²的值吗？

有下列各有理数：﹣2²，﹣|﹣2．5|，，0，（﹣1）¹⁰⁰，﹣|3|．
（1）将上述各数填入适当的括号内．
正整数：{                }；负有理数：{                      }
（2）将上面各数在数轴上表示出来，并按从小到大的顺序用“＜”号连接起来．

（本题10分）如图，数轴上的三点A、B、C分别表示有理数a、b、c．（O为原点）

（1）a－b      0，a＋c      0，b－c      0．
（用“＜”或“＞”或“=”号填空）
化简：|a－b|－|a＋c|＋|b－c|
（2）若数轴上两点A、B对应的数分别为－3、－1，点P为数轴上一动点，其对应的数为x．
①若点P到点A、点B的距离相等，则点P对应的数x为          ；
②若点A、点B分别以2个单位长度/秒和0．5个单位长度/秒的速度同时向右运动，点P以6个单位长
度/秒的速度同时从原点O向左运动．当点A与点B之间的距离为1个单位长度时，求点P所对应的数
x是多少？

（本题8分）已知：，，当x取何值时
（1）y₁与y₂互为相反数？
（2）y₁比y₂小2？

解方程（每题4分，共8分）
（1）    （2）－

在抗洪抢险中，人民解放军的冲锋舟沿东西方向的河流抢救灾民，早晨从A地出发，晚工到达B地，约定向东为正方向，当天航行路程记录如下：14，-9，-18，-7，13，-6，10，-5（单位：千米）．
（1）B地在A地何位置？
（2）若冲锋舟每千米耗油0．5升，出发前冲锋舟油箱有油29升，求途中需补充多少升油？

（本题10分）某商品的进价为每件30元，现在的售价为每件40元，每星期可卖出150件．市场调查反映：如果每件的售价每涨1元（售价每件不能高于45元），那么每星期少卖10件．设每件涨价x元（x为非负整数），每星期的销量为y件．
（1）求y与x的函数关系式及自变量x的取值范围；
（2）如何定价才能使每星期的利润最大且每星期的销量较大？每星期的最大利润是多少？

（本题8分）如图1，在一个不透明的袋子中装有四个球，分别标有字母A、B、C、D，这些球除了字母外完全相同，此外，有一面白色、另一面黑色、大小相同的四张正方形卡片，每张卡片两面的字母相同，分别标有字母A、B、C、D．最初，摆成如图2的样子，A．D是黑色，B．C是白色．

两次操作后观察卡片的颜色．
（如：第一次取出A、第二次取出B，此时卡片的颜色变成）
（1）求取四张卡片变成相同颜色的概率；
（2）求四张卡片变成两黑两白、并恰好形成各自颜色的矩形的概率．

（本题8分）如图，AB是⊙O的直径，C．D两点在⊙O上，若∠C＝45°．

（1）求∠ABD的度数；
（2）若∠CDB=30°，BC=3，求⊙O的半径．

（本小题满分6分）先化简，再求值：，其中是不等式组的整数解．

已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A，C的坐标分别为A（﹣3，0），C（1，0），tan∠BAC=．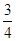

（1）写出点B的坐标；
（2）在x轴上找一点D，连接BD，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；
（3）在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP=DQ=m，问是否存在这样的m使得△APQ与△ADB相似？如存在，请求出的m值；如不存在，请说明理由．

（本小题8分）已知抛物线．
（1）求证：此抛物线与x轴必有两个不同的交点；
（2）若此抛物线与直线的一个交点在y轴上，求m的值．

关于x的一元二次方程（a-6）x²-8x+9=0有实根．
（1）求a的最大整数值；
（2）当a取最大整数值时，
①求出该方程的根；
②求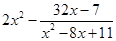的值．

如图，已知直线PA交⊙O于A、B两点，AE是⊙O的直径，点C为⊙O上一点，且AC平分∠PAE，过C作CD丄PA，垂足为D．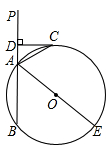

（1）CD为⊙O的切线吗，说明理由；
（2）若DC+DA=6，⊙O的直径为10，求AB的长度．