初中数学解答题

（1）证明：不论取什么值，直线：y＝x-都通过一个定点；
（2）以A（0，2）、B（2，0）、O（0，0）为顶点的三角形被直线分成两部分，分别求出当=２和=－时，靠近原点O一侧的那部分面积．

（1）如图1，为的角平分线，于，于，，请补全图形，并求与的面积的比值；

（2）如图2，分别以的边、为边向外作等边三角形和等边三角形，与相交于点，判断与的数量关系，并证明；
（3）在四边形中，已知，且，对角线平分，
请直接写出和的数量关系.

小明在上物理实验课时，利用量筒和体积相同的小球进行了如下操作：

请根据示意图中所给信息，解答下列问题：
（1）放入一个小球后，量筒中水面升高cm；
（2）求放入小球后，量筒中水面的高度（cm）与小球个数（个）之间的函数关系式（不要求写出自变量的取值范围）；
（3）若往量筒中继续放入小球，量筒中的水就会溢出．问：量筒中至少放入几个小球时有水溢出？

小颖和小亮上山游玩，小颖乘会缆车，小亮步行，两人相约在山顶的缆车终点会合．已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍，小颖在小亮出发后50 min才乘上缆车，缆车的平均速度为180 m/min．设小亮出发x min后行走的路程为y m．图中的折线表示小亮在整个行走过程中y与x的函数关系．
⑴小亮行走的总路程是____________㎝，他途中休息了________min．
⑵①当50≤x≤80时，求y与x的函数关系式；
②当小颖到达缆车终点为时，小亮离缆车终点的路程是多少？

如图，在直角梯形ABCD中，AD∥BC，，AD=6，BC=8，，点M是BC的中点．点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动，到达点B后立刻以原速度沿BM返回；点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动．在点P，Q的运动过程中，以PQ为边作等边三角形EPQ，使它与梯形ABCD在射线BC的同侧．点P，Q同时出发，当点P返回到点M时停止运动，点Q也随之停止．设点P，Q运动的时间是t秒(t＞0)．
（1）设PQ的长为y，在点P从点M向点B运动的过程中，写出y与t之间的函数关系式（不必写t的取值范围）．
（2）当BP=1时，求△EPQ与梯形ABCD重叠部分的面积．
（3）随着时间t的变化，线段AD会有一部分被△EPQ覆盖，被覆盖线段的长度在某个时刻会达到最大值，请回答：该最大值能否持续一个时段？若能，直接写出t的取值范围；若不能，请说明理由．

如图，正方形ABCD的四个顶点分别在四条平行线、、、上，这四条直线中相邻两条之间的距离依次为、、（＞0，＞0，＞0）．
（1）求证：=；
（2）设正方形ABCD的面积为S，求证：S=；
（3）若，当变化时，说明正方形ABCD的面积S随的变化情况．

在平面直角坐标系中，抛物线与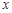轴的两个交点分别为A（-3，0）、B（1，0），过顶点C作CH⊥x轴于点H.
（1）求抛物线的解析式和顶点坐标；
（2）在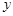轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标.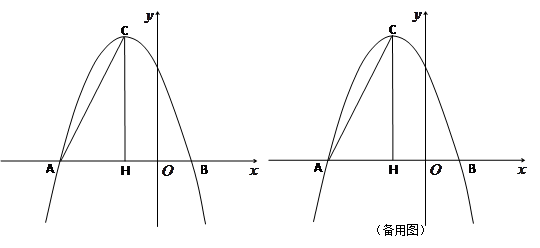

如图，长为2，宽为的矩形纸片（），剪去一个边长等于矩形宽度的正方形（称为第一次操作）；
（1）第一次操作后剩下的矩形长为，宽为；
（2）再把第一次操作后剩下的矩形剪去一个边长等于此时矩形宽度的正方形（称为第二次操作）；如此反复操作下去．
①求第二次操作后剩下的矩形的面积；
②若在第3次操作后，剩下的图形恰好是正方形，求的值．

阳光公司决定按左图给出的比例，从甲、乙、丙三个工厂共购买200件同种产品A，已知这三个工厂生产的产品A的优品率如下表所示．

	甲	乙	丙
优品率	80%	85%	90%

⑴阳光公司从甲厂应购买件产品Ａ，从乙厂应购买件产品Ａ，从丙厂应购买件产品Ａ；
⑵阳光公司所购买的200件产品A的优品率为；
⑶你认为阳光公司能否通过调整从三个工厂所购买的产品A的比例（每个工厂的购买数均大于0），使所购买的200件产品A的优品率上升3%．若能，请问应从甲厂购买多少件产品A；若不能，请说明理由．

如图，在△ABC和△DEF中，AC∥DE，∠EFD与∠B互补，DE=mAC（m＞1）．试探索线
段EF与AB的数量关系，并证明你的结论．

如图，在等腰梯形ABCD中，∠B=60º，且AB=AD=CD，请你将等腰梯形分成3个三角形，
使得其中有两个是相似三角形，且相似比不为1．
现在请你参考示意图，另外再给出三种分割方法（注：在两个相似三角形中标明必要的角度．）

已知圆锥的底面积和它的侧面积之比为，求侧面展开后所得扇形的圆心角的度数。

如图，在△ABC中，∠C＝90º，AC＝6cm，BC＝8cm，D、E分别是AC、AB
的中点，连接DE．点P从点D出发，沿DE方向匀速运动，速度为1cm/s；同时，点Q从点B出发，沿
BA方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t(0＜t
＜4)s．解答下列问题：

(1)当t为何值时，PQ⊥AB？
(2)当点Q在B、E之间运动时，设五边形PQBCD的面积为ycm²，求y与t之间的函数关系式；
(3)在(2)的情况下，是否存在某一时刻t，使得PQ分四边形BCDE所成的两部分的面积之比为
＝1∶29？若存在，求出此时t的值以及点E到PQ的距离h；若不存在，请说明理由．

已知抛物线经过A（2，0）． 设顶点为点P，与x轴的另一交点为点B．
（1）求b的值，求出点P、点B的坐标；
（2）如图，在直线 上是否存在点D，使四边形OPBD为平行四边形？若存在，求出点D的坐
标；若不存在，请说明理由；
（3）在x轴下方的抛物线上是否存在点M，使△AMP≌△AMB？如果存在，试举例验证你的猜想；如果不存在，试说明理由．

如图所示，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点（不与点A、点D重合）将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH．
（1）求证：∠APB=∠BPH；
（2）当点P在边AD上移动时，△PDH的周长是否发生变化？并证明你的结论；
（3）设AP为x，四边形EFGP的面积为S，求出S与x的函数关系式，试问S是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．