如图,平面直角坐标系 中,已知点
中,已知点 (2,3),线段
(2,3),线段 垂直于
垂直于 轴,垂足为
轴,垂足为 ,将线段
,将线段 绕点A逆时针方向旋转
绕点A逆时针方向旋转 ,点
,点 落在点
落在点 处,直线
处,直线 与
与 轴的交于点
轴的交于点 .
.
(1)试求出点 的坐标;
的坐标;
(2)试求经过 、
、 、
、 三点的抛物线的表达式,并写出其顶点E的坐标;
三点的抛物线的表达式,并写出其顶点E的坐标;
(3)在(2)中所求抛物线的对称轴上找点 ,使得以点
,使得以点 、
、 、
、 为顶点的三角形与△
为顶点的三角形与△ 相似.
相似.
函数 和
和
 的图像关于
的图像关于 轴对称,我们把函数
轴对称,我们把函数 和
和
 叫做互为“镜子”函数.类似地,如果函数
叫做互为“镜子”函数.类似地,如果函数 和
和 的图像关于
的图像关于 轴对称,那么我们就把函数
轴对称,那么我们就把函数 和
和 叫做互为“镜子”函数.
叫做互为“镜子”函数.
(1)请写出函数 的“镜子”函数:,
的“镜子”函数:,
(2)函数的“镜子”函数是 ;
;
(3)如图7,一条直线与一对“镜子”函数 (
( >
> )和
)和 (
( <
< )的图像分别交于点
)的图像分别交于点 ,如果
,如果 ,点
,点 在函数
在函数 (
( <
< )的“镜子”函数上的对应点的横坐标是
)的“镜子”函数上的对应点的横坐标是 ,求点
,求点 的坐标.
的坐标.
如图,在
 中,
中, ,
, ,点
,点 在
在 边上(点
边上(点 与点
与点 、
、 不重合),
不重合), ∥
∥ 交
交 边与点
边与点 ,点
,点 在线段
在线段 上,且
上,且 ,以
,以 、
、 为邻边作平行四边形
为邻边作平行四边形 联结
联结 .
.
(1)当 时,求
时,求
 的面积;
的面积;
(2)设 ,
,
 的面积为
的面积为 ,求
,求 与
与 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)如果
 是以
是以 为腰的等腰三角形,求
为腰的等腰三角形,求 的值.
的值.
已知直线 分别与
分别与 轴、
轴、 轴交于点
轴交于点 、
、 ,抛物线
,抛物线 经过点
经过点 、
、 .
.
(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
(2)记该抛物线的对称轴为直线 ,点
,点 关于直线
关于直线 的对称点为
的对称点为 ,若点
,若点 在
在 轴的正半轴上,且四边形
轴的正半轴上,且四边形 为梯形.
为梯形.
① 求点 的坐标;
的坐标;
② 将此抛物线向右平移,平移后抛物线的顶点为 ,其对称轴与直线
,其对称轴与直线 交于点
交于点 ,若tan
,若tan
 =
= ,求四边形
,求四边形 的面积.
的面积.
某公园有一圆弧形的拱桥,如图已知拱桥所在的圆的半径为10米,拱桥顶 到水面
到水面 距离
距离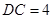 米.
米.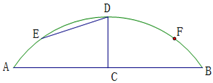
(1)求水面宽度 的大小;
的大小;
(2)当水面上升到 时,从点
时,从点 测得桥顶
测得桥顶 的仰角为
的仰角为 ,若
,若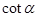 =3,求水面上升的高度.
=3,求水面上升的高度.
如图,直线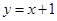 与
与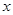 轴、
轴、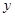 轴分别相交于点
轴分别相交于点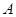 、
、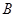 .抛物线
.抛物线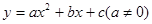 与
与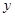 轴的正半轴相交于点
轴的正半轴相交于点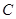 ,与这个一次函数的图像相交于
,与这个一次函数的图像相交于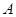 、
、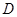 ,且
,且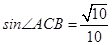 .
.
(1)求点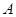 、
、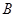 、
、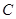 的坐标;
的坐标;
(2)如果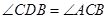 ,求抛物线
,求抛物线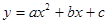 的解析式.
的解析式.
下面提供上海楼市近期的两幅业务图:图(甲)所示为2011年6月至12月上海商品房平均成交价格的走势图(单位:万元/平方米);图(乙)所示为2011年12月上海商品房成交价格段比例分布图(其中 为每平方米商品房成交价格,单位:万元/平方米).
为每平方米商品房成交价格,单位:万元/平方米).
(1)根据图(甲),写出2011年6月至2011年12月上海商品房平均成交价格的中位数;
(2)根据图(乙),可知x=;
(3)2011年12月从上海市的内环线以内、内中环之间、中外环之间和外环线以外等四个区域中的每个区域的在售楼盘中随机抽出两个进行分析:共有可售商品房2400套,其中成交200套.请估计12月份在全市所有的60000套可售商品房中已成交的并且每平方米价格低于2万元的商品房的套数.
如图, 中,
中, ,
, ,过点
,过点 作
作 ∥
∥ ,点
,点 、
、 分别是射线
分别是射线 、线段
、线段 上的动点,且
上的动点,且 ,过点
,过点 作
作 ∥
∥ 交线段
交线段 于点
于点 ,联接
,联接 ,设
,设 面积为
面积为 ,
, .
.
(1)用 的代数式表示
的代数式表示 ;
;
(2)求 与
与 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(3)联接 ,若
,若 与
与 相似,求
相似,求 的长.
的长.
已知:如图, ⊥
⊥ ,
, ∥
∥ ,
, ,
, .点
.点 在线段
在线段 上,联结
上,联结 ,过点
,过点 作
作 的垂线,与
的垂线,与 相交于点
相交于点 .设线段
.设线段 的长为
的长为 .
.
(1)当 时,求线段
时,求线段 的长;
的长;
(2)设△ 的面积为
的面积为 ,求
,求 关于
关于 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(3)当△ ∽△
∽△ 时,求线段
时,求线段 的长.
的长.

已知 是最小的正整数,b、c互为倒数,|b|+b=0,|c|=
是最小的正整数,b、c互为倒数,|b|+b=0,|c|= ,求式子
,求式子 的值。
的值。
为了向国庆献礼,某校各班都在开展丰富多彩的庆祝活动,八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20 cm,宽AB=16 cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处(如图),…请你根据①②步骤解答下列问题:(1)计算BF的长;(2)计算EC的长.
平面直角坐标系中,正方形AOBC如图所示,点C的坐标为(a,a),其中a使得式子 有意义,反比例函数
有意义,反比例函数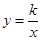 的图象经过点C.
的图象经过点C.
(1)求反比例函数解析式.
(2)若有一点D自A向O运动,当满足AD2=OD·AO时,求此时D点坐标.
(3)若点D在AO上、G为OB的延长线上的点,AD=BG,连接AB交DG于点H,写出AB-2HB与AD之间的数量关系(直接写出不需证明).
(4)如图,点E为正方形AOBC的OB边一点,点F为BC上一点且∠CAE=∠FEA=60°,求直线EF的解析式.
试题篮
()