如图1,点 将线段
将线段 分成两部分,如果
分成两部分,如果 ,那么称点
,那么称点 为线段
为线段 的黄金分割点.
的黄金分割点.
某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线 将一个面积为
将一个面积为 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为 ,
, ,如果
,如果 ,那么称直线
,那么称直线 为该图形的黄金分割线.
为该图形的黄金分割线.
(1)研究小组猜想:在 中,若点
中,若点 为
为 边上的黄金分割点(如图2),则直线
边上的黄金分割点(如图2),则直线 是
是 的黄金分割线.你认为对吗?为什么?
的黄金分割线.你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组在进一步探究中发现:过点 任作一条直线交
任作一条直线交 于点
于点 ,再过点
,再过点 作直线
作直线 ,交
,交 于点
于点 ,连接
,连接 (如图3),则直线
(如图3),则直线 也是
也是 的黄金分割线.
的黄金分割线.
请你说明理由.
(4)如图4,点 是
是 的边
的边 的黄金分割点,过点
的黄金分割点,过点 作
作 ,交
,交 于点
于点 ,显然直线
,显然直线 是
是 的黄金分割线.请你画一条
的黄金分割线.请你画一条 的黄金分割线,使它不经过
的黄金分割线,使它不经过 各边黄金分割点.
各边黄金分割点.
在平面内,先将一个多边形以点 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点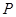 ,它的对应点
,它的对应点 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为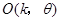 ,其中点
,其中点 叫做旋转相似中心,
叫做旋转相似中心, 叫做相似比,
叫做相似比, 叫做旋转角.
叫做旋转角.
(1)填空:
①如图1,将 以点
以点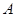 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为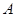 (,);
(,);
②如图2, 是边长为
是边长为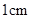 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到 ,则线段
,则线段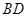 的长为
的长为 ;
;
(2)如图3,分别以锐角三角形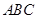 的三边
的三边 ,
,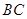 ,
, 为边向外作正方形
为边向外作正方形 ,
, ,
,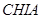 ,点
,点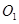 ,
, ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与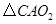 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与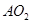 之间的关系.
之间的关系.
在梯形 中,
中, ,
, ,
, ,点
,点 分别在线段
分别在线段 上(点
上(点 与点
与点 不重合),且
不重合),且 ,设
,设 ,
, .
.
(1)求 与
与 的函数表达式;
的函数表达式;
(2)当 为何值时,
为何值时, 有最大值,最大值是多少?
有最大值,最大值是多少?
如图一,平面直角坐标系中有一张矩形纸片OABC,O为坐标原点,A点坐标为(10,0),C点坐标为(0,6),D是BC边上的动点(与点B,C不重合),现将△COD沿OD翻折,得到△FOD;再在AB边上选取适当的点E,将△BDE沿DE翻折,得到△GDE,并使直线DG、DF重合。
(1)如图二,若翻折后点F落在OA边上,求直线DE的函数关系式;
(2)设D(a,6),E(10,b),求b关于a的函数关系式,并求b的最小值;
(3)一般地,请你猜想直线DE与抛物线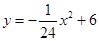 的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线
的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线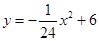 始终有公共点,请在图一中作出这样的公共点。
始终有公共点,请在图一中作出这样的公共点。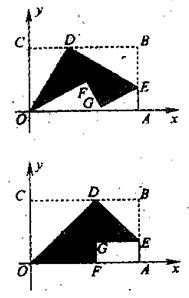
如图,在平面直角坐标系中,点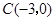 ,点
,点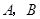 分别在
分别在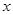 轴,
轴,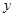 轴的正半轴上,且满足
轴的正半轴上,且满足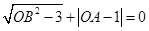 .
.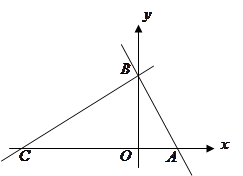
(1)求点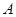 ,点
,点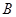 的坐标.
的坐标.
(2)若点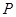 从
从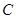 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线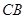 运动,连结
运动,连结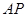 .设
.设 的面积为
的面积为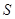 ,点
,点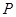 的运动时间为
的运动时间为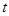 秒,求
秒,求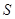 与
与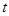 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点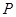 ,使以点
,使以点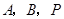 为顶点的三角形与
为顶点的三角形与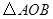 相似?若存在,请直接写出点
相似?若存在,请直接写出点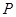 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
如图,抛物线 与
与 轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当
轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当 =O和
=O和 =4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
=4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
(1)求这条抛物线的解析式;
(2)P为线段OM上一点,过点P作PQ⊥ 轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
(3)随着点P的运动,四边形PQCO的面积S有最大值吗?如果S有最大值,请求出S的最大值并指出点Q的具体位置和四边形PQCO的特殊形状;如果S没有最大值,请简要说明理由;
(4)随着点P的运动,是否存在t的某个值,能满足PO=OC?如果存在,请求出t的值。
如图①, 中,
中, ,
, .它的顶点
.它的顶点 的坐标为
的坐标为 ,顶点
,顶点 的坐标为
的坐标为 ,
, ,点
,点 从点
从点 出发,沿
出发,沿 的方向匀速运动,同时点
的方向匀速运动,同时点 从点
从点 出发,沿
出发,沿 轴正方向以相同速度运动,当点
轴正方向以相同速度运动,当点 到达点
到达点 时,两点同时停止运动,设运动的时间为
时,两点同时停止运动,设运动的时间为 秒.
秒.
(1)求 的度数.
的度数.
(2)当点 在
在 上运动时,
上运动时, 的面积
的面积 (平方单位)与时间
(平方单位)与时间 (秒)之间的函数图象为抛物线的一部分,(如图②),求点
(秒)之间的函数图象为抛物线的一部分,(如图②),求点 的运动速度.
的运动速度.
(3)求(2)中面积 与时间
与时间 之间的函数关系式及面积
之间的函数关系式及面积 取最大值时点
取最大值时点 的坐标.
的坐标.
(4)如果点 保持(2)中的速度不变,那么点
保持(2)中的速度不变,那么点 沿
沿 边运动时,
边运动时, 的大小随着时间
的大小随着时间 的增大而增大;沿着
的增大而增大;沿着 边运动时,
边运动时, 的大小随着时间
的大小随着时间 的增大而减小,当点
的增大而减小,当点 沿这两边运动时,使
沿这两边运动时,使 的点
的点 有几个?请说明理由.
有几个?请说明理由.
某学校七年级数学兴趣小组组织一次数学活动.在一座有三道环形路的数字迷宫的每个进口处都标记着一个数,要求进入者把自己当做数“1”,进入时必须乘进口处的数,并将结果带到下一个进口,依次累乘下去,在通过最后一个进口时,只有乘积是5的倍数,才可以进入迷宫中心,现让一名5岁小朋友小军从最外环任一个进口进入.
(1)小军能进入迷宫中心的概率是多少?请画出树状图进行说明.
(2)小组两位组员小张和小李商量做一个小游戏,以猜测小军进迷宫的结果比胜负.游戏规则规完:小军如果能进入迷宫中心,小张和小李各得1分;小军如果不能进入迷宫中心,则他在最后一个进口处所得乘积是奇数时,小张得3分,所得乘积是偶数时,小李得3分,你认为这个游戏公平吗?如果公平,请说明理由;如果不公平,请在第二道环进口处的两个数中改变其中一个数使游戏公平.
(3)在(2)的游戏规则下,让小军从最外环进口任意进入10次,最终小张和小李的总得分之和不超过28分,请问小军至少几次进入迷宫中心?
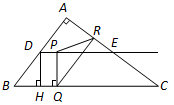
如图,在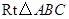 中,
中,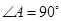 ,
,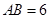 ,
,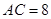 ,
,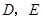 分别是边
分别是边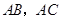 的中点,点
的中点,点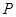 从点
从点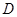 出发沿
出发沿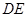 方向运动,过点
方向运动,过点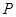 作
作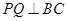 于
于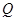 ,过点
,过点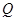 作
作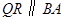 交
交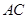 于
于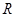 ,当点
,当点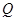 与点
与点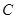 重合时,点
重合时,点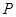 停止运动.设
停止运动.设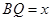 ,
,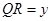 .
.
(1)求点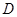 到
到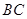 的距离
的距离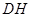 的长;
的长;
(2)求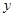 关于
关于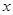 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点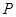 ,使
,使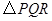 为等腰三角形?若存在,请求出所有满足要求的
为等腰三角形?若存在,请求出所有满足要求的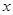 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
一次函数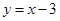 的图象与
的图象与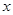 轴,
轴,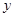 轴分别交于点
轴分别交于点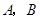 .一个二次函数
.一个二次函数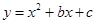 的图象经过点
的图象经过点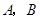 .
.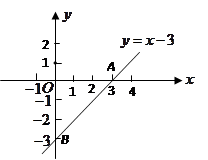
(1)求点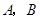 的坐标,并画出一次函数
的坐标,并画出一次函数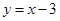 的图象;
的图象;
(2)求二次函数的解析式及它的最小值.
如图①,正方形 的顶点
的顶点 的坐标分别为
的坐标分别为 ,顶点
,顶点 在第一象限.点
在第一象限.点 从点
从点 出发,沿正方形按逆时针方向匀速运动,同时,点
出发,沿正方形按逆时针方向匀速运动,同时,点 从点
从点 出发,沿
出发,沿 轴正方向以相同速度运动.当点
轴正方向以相同速度运动.当点 到达点
到达点 时,
时, 两点同时停止运动,设运动的时间为
两点同时停止运动,设运动的时间为 秒.
秒.
(1)求正方形 的边长.
的边长.
(2)当点 在
在 边上运动时,
边上运动时, 的面积
的面积 (平方单位)与时间
(平方单位)与时间 (秒)之间的函数图象为抛物线的一部分(如图②所示),求
(秒)之间的函数图象为抛物线的一部分(如图②所示),求 两点的运动速度.
两点的运动速度.
(3)求(2)中面积 (平方单位)与时间
(平方单位)与时间 (秒)的函数关系式及面积
(秒)的函数关系式及面积 取最大值时点
取最大值时点 的坐标.
的坐标.
(4)若点 保持(2)中的速度不变,则点
保持(2)中的速度不变,则点 沿着
沿着 边运动时,
边运动时, 的大小随着时间
的大小随着时间 的增大而增大;沿着
的增大而增大;沿着 边运动时,
边运动时, 的大小随着时间
的大小随着时间 的增大而减小.当点
的增大而减小.当点 沿着这两边运动时,使
沿着这两边运动时,使 的点
的点 有 个.
有 个.
(抛物线 的顶点坐标是
的顶点坐标是 .)
.)
如图,在平面直角坐标系内,⊙C与y轴相切于D点,与x轴相交于A(2,0)、B(8,0)两点,圆心C在第四象限.
⑴ 求点C的坐标;
⑵ 连结BC并延长交⊙C于另一点E,若线段BE上有一点P,使得AB2=BP·BE,能否推出AP⊥BE?请给出你的结论,并说明理由;
⑶ 在直线BE上是否存在点Q,使得AQ2=BQ·EQ?若存在,求出点Q的坐标;若不存在,也请说明理由.
如图 ,梯形
,梯形 中,
中, ∥
∥ ,
, ,
, ,
, .动点
.动点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度在线段
个单位长度的速度在线段 上运动;动点
上运动;动点 同时从点
同时从点 出发,以每秒
出发,以每秒 个单位长度的速度在线段
个单位长度的速度在线段 上运动.以
上运动.以 为边作等边△
为边作等边△ ,与梯形
,与梯形 在线段
在线段 的同侧.设点
的同侧.设点 、
、 运动时间为
运动时间为 ,当点
,当点 到达
到达 点时,运动结束.
点时,运动结束.
(1)当等边△ 的边
的边 恰好经过点
恰好经过点 时,求运动时间
时,求运动时间 的值;
的值;
(2)在整个运动过程中,设等边△ 与梯形
与梯形 的重合部分面积为
的重合部分面积为 ,请直接写出
,请直接写出 与
与 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量 的取值范围;
的取值范围;
(3)如图 ,当点
,当点 到达
到达 点时,将等边△
点时,将等边△ 绕点
绕点 旋转
旋转 (
( ),
),
直线 分别与直线
分别与直线 、直线
、直线 交于点
交于点 、
、 .是否存在这样的
.是否存在这样的 ,使△
,使△ 为等腰三角形?若存在,请求出此时线段
为等腰三角形?若存在,请求出此时线段 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
如图是一个“有理数转换器”(箭头是指数进入转换器的路径,方框是对进入的数进行转换的转换器)
(1)当小明输入3;—4, ;—201这四个数时,这四次输出的结果分别是:
;—201这四个数时,这四次输出的结果分别是:
(2)你认为当输入什么数时,其输出结果是0 ?
(3)你认为这个“有理数转换器”不可能输出什么数?
(4)有一次,小明在操作的时候,输出的结果是2,你判断一下,小明可能输入的是什么数?
试题篮
()