初中数学解答题

某商场为了吸引顾客，设计了一个摸球获奖的箱子，箱子中共有20个球，其中红球2个，兰球3个，黄球5个，白球10个，并规定购买100元的商品，就有一次摸球的机会，摸到红、兰、黄、白球的(一次只能摸一个)，顾客就可以分别得到80元、30元、10元、0元购物卷，凭购物卷仍然可以在商场购买，如果顾客不愿意摸球，那么可以直接获得购物卷10元.
(1)每摸一次球所获购物卷金额的平均值是多少？
(2)你若在此商场购买100元的货物，两种方式中你应选择哪种方式？为什么？

如图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC，AD，BD的长．

阅读材料：如图①，一扇窗户打开后用窗钩可将其固定．

（1）这里所运用的几何原理是（）

A．三角形的稳定性	B．两点之间线段最短
C．两点确定一条直线	D．垂线段最短

（2）如图②是图①中窗子开到一定位置时的平面图，若，,=60cm，求点到边的距离．（结果保留根号）

如图，要在一块形状为直角三角形（∠C为直角）的铁皮上裁出一个半圆形的铁皮，需先在这块铁皮上画出一个半圆，使它的圆心在线段AC上，且与AB、BC都相切.请你用直尺和圆规画出来（要求用尺规作图，保留作图痕迹，不要求写作法）．

在平面直角坐标系中，给定以下五点A（－2，0），B（1，0）C（4，0），D（－2，），E（0，－6），从这五点中选取三点，使经过这三点的抛物线满足以平行于y轴的直线为对称轴．我们约定：把经过三点A、E、B的抛物线表示为抛物线AEB（如图所示）．

（1）问符合条件的抛物线还有哪几条？不求解析式，请用约定的方法一一表示出来；
（2）在（1）中是否存在这样的一条抛物线，它与余下的两点所确定的直线不相交？如果存在，试求出抛物线及直线的解析式；如果不存在，请说明理由．

某生物兴趣小组在四天的实验研究中发现：骆驼的体温会随外部环境温度的变化而变化，而且在这四天中每昼夜的体温变化情况相同．他们将一头骆驼前两昼夜的体温变化情况绘制成下图．请根据图象回答：

⑴第一天中，在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多少时间?
⑵第三天12时这头骆驼的体温是多少?
⑶兴趣小组又在研究中发现，图中10时到22时的曲线是抛物线，求该抛物线的解析式

如图，把直角梯形沿方向平移得到梯形，与相交于点，=20cm，=5cm，=4cm，图中阴影部分的面积与哪个四边形的面积相等，并求出阴影部分的面积

如图，若要在长32m，宽20m的长方形地面上修筑同样宽2米的两条道路，余下的部分修草坪，草坪的面积是多少？

某商场重新装修后，准备在大厅的主楼梯上铺设一种红色的地毯，已知地毯每平方米40元，主楼梯道的宽为3米，问买地毯至少需要多少元？

如图，将沿方向平移距离得到，已知=5，=8，=3，求图中阴影部分面积。

如图，是一块钜形的场地，长=101米，宽=52米，从、两处入口的中路宽都为1米，两小路汇合处路口宽为2米，其余部分种植草坪面积为___米2

如图
（1）请写出在直角坐标系中的房子的A、B、C、D、E、F、G的坐标。
（2）源源想把房子向下平移3个单位长度，你能帮他办到吗？请作出相应图案，并写出平移后的7个点的坐标。

如图 (1) ，将平行四边形ABCD向左平移2个单位长度，可以得到A’B’C’D’，画出平移后的图形，并指出其各个顶点的坐标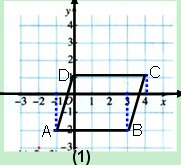

小红是某中学的七年级学生，放学后从学校骑自行车回家，学校在她现在位置的北偏东30°方向，距离此处1.5km的地方，她的家在她现在的位置的南偏西45°的方向，距离此处2km，邮局在她现在的位置的北偏西60°的方向，距离此处3km。根据这些信息画一张表示各处位置的简图

已知：矩形ABCD的顶点坐标为A（1，1），B（2，1），C（2，3），D（1，3）在平面直角坐标系标出个点。
（1）将矩形向上平移2个单位，画出相应的图形，并写出各点的坐标；
（2）将矩形各顶点的横、纵坐标都乘以－1，画出相应的图形；
（3）在（1）、（2）中，你发现了什么？