初中数学解答题

崀山成功列入世界自然遗产名录后，景区管理部门决定在八角寨架设旅游索道．设计人员为了计算索道AB（索道起点为山脚B处，终点为山顶A处）的长度，采取了如图（八）所示的测量方法．在B处测得山顶A的仰角为16°，查阅相关资料得山高AC＝325米，求索道AB的长度．（结果精确到1米）
       

在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点，顺次连接EF、FG、GH、HE．
（1）请判断四边形EFGH的形状，并给予证明；
（2）试添加一个条件，使四边形EFGH是菱形．(写出你添加的条件，不要求证明)
             

如图，已知O是平面直角坐标系的原点，半径为1的⊙B经过点O，且与x、y
轴分别交于点A、C，点A的坐标为（-，0），AC的延长线与⊙B的切线OD
交于点D.
（1）求OC的长和∠CAO的度数；
（2）求点D的坐标；
（3）求过点A，O，D三点的抛物线的解析式；
（4）在（3）中，点P是抛物线上的一点，试确定点P的位置，使得△AOP的
面积与△AOC的面积相等.

在△ABC中，BC=6，AC=4，∠C=45^o，在BC上有一动点P，过P作PD∥BA与AC相交于点D，连结AP，设BP=x，△APD的面积为y.
（1）求y与x之间的函数关系式，并指出自变量x的取值范围；
（2）是否存在点P，使△APD的面积最大？若存在，求出BP的长，并求出
△APD面积的最大值.

甲乙两人在玩转盘游戏时，把转盘A、B分别分成4等份、3等份，并在每一份内标上数字，如图所示. 游戏规定，转动两个转盘停止后，指针必须指到某一数字，否则重转。

（1）请用树状图或列表法列出所有可能的结果；
（2）若指针所指的两个数字都是方程x²-4x+3=0的解时，则甲获胜；若指针所指的两个数字都不是方程x²-4x+3=0的解时，则乙获胜．问他们两人谁获胜的概率大?请分析说明。

（本题7分）（1）如图，⊿ABC的三个顶点坐标
分别为A（－1， 1）、B（－2，3）、C（－1，3），
(1) 将⊿ABC沿x轴正方向平移2个单位得到⊿A₁B₁C₁，
请在网格中画出
（2）⊿A₁B₁C₁绕点（0，1）顺时针旋转90°得到⊿A₂B₂C₂，
则直线A₂B₂的解析式是        .

已知，如图，AB∥ED，点F、点C在AD上，AB=DE,AF=DC.
求证：BC="EF."

先化简，再求值：，其中

解方程：.

（本小题满分8分）如图，在平面直角坐标系中，点O是坐标原点，四边形AOCB是梯形，AB∥OC，点A在y轴上，点C在x轴上，且，OB＝OC．
（1）求点B的坐标；
（2）点P从C点出发，沿线段CO以5个单位/秒的速度向终点O匀速运动，过点P作PH⊥OB，垂足为H，设△HBP的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式（直接写出自变量t的取值范围）；
（3）在（2）的条件下，过点P作PM∥CB交线段AB于点M，过点M作MR⊥OC，垂足为R，线段MR分别交直线PH、OB于点E、G，点F为线段PM的中点，联结EF．
①判断EF与PM的位置关系；
②当t为何值时，？

（本小题满分7分）如图，已知二次函数的图象与x轴负半轴交于点A（-1，0），与y轴正半轴交与点B，顶点为P，且OB=3OA，一次函数y=kx+b的图象经过A、B．

（1）求一次函数解析式；
（2）求顶点P的坐标；
（3）平移直线AB使其过点P，如果点Ｍ在平移后的直线上，且，求点M坐标；
（４）设抛物线的对称轴交x轴与点E，联结AP交y轴与点D，若点Q、N分别为两线段PE、PD上的动点，联结QD、QN，请直接写出QD+QN的最小值．

（本小题满分7分）已知：二次函数y=．
（1）求证：此二次函数与x轴有交点；
（2）若m-1=0,求证方程有一个实数根为1；
（3）在（2）的条件下，设方程的另一根为a,当x=2时，关于n 的函数与的图象交于点A、B（点A在点B的左侧），平行于y轴的直线L与、的图象分别交于点C、D，若CD=6，求点C、D的坐标.

（本小题满分5分）已知菱形纸片ABCD的边长为，∠A=60°，E为边上的点，过点E作EF∥BD交AD于点F．将菱形先沿EF按图1所示方式折叠，点A落在点处，过点作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠，点C落在点处，与H分别交与于点M、N．若点在△EF的内部或边上，此时我们称四边形（即图中阴影部分）为“重叠四边形”．

 
图1                      图2                     备用图
（1）若把菱形纸片ABCD放在菱形网格中（图中每个小三角形都是边长为1的等边三角形），点A、B、C、D、E恰好落在网格图中的格点上．如图2所示，请直接写出此时重叠四边形的面积；
（2）实验探究：设AE的长为，若重叠四边形存在．试用含的代数式表示重叠四边形的面积，并写出的取值范围（直接写出结果，备用图供实验，探究使用）．

（本小题满分5分）“校园手机”现象越来越受到社会的关注．“春节”期间，小记者刘凯随机调查了我区若干名学生和家长对中学生带手机现象的看法，统计整理并制作了如下的统计图：

 
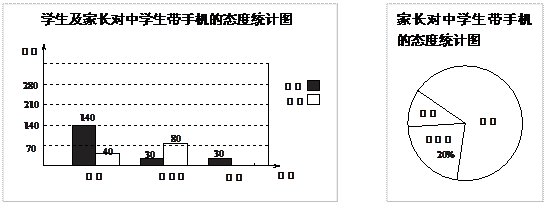图①                                图②
（1）求这次调查的家长人数，并补全图①；
（2）求图②中表示家长“赞成”的圆心角的度数；
（3）从这次接受调查的学生中，随机抽查一个，恰好是“无所谓”态度的学生的概率是多少？

（本小题满分5分）已知：如图，在中，，点在上，以为圆心，长为半径的圆与分别交于点，且．
（1）判断直线与的位置关系，并证明你的结论；
（2）若，=，求的值．