初中数学解答题

如图，在平面直角坐标系中，抛物线向左平移1个单位，再向下平移4个单位，得到抛物线.所得抛物线与轴交于两点（点在点的左边），与轴交于点，顶点为.
（1）求的值；
（2）求直线AC的函数解析式。
（3）在线段上是否存在点，使与相似.若存在，求出点的坐标；若不存在，说明理由.

（满分11分）如图11，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于F，连结CF.
（1）求证：AF=CD；
（2）若AB=AC，∠BAC=90°，试判断四边形ADCF的形状，并证明你的结论；
（3）在（2）的条件下，求sin∠ABF的值.

、(本题12分)如图甲，在△ABC中，E是AC边上的一点，
(1)在图甲中，作出以BE为对角线的平行四边形BDEF，使D、F分别在BC和AB边上；
(2)改变点E的位置，则图甲中所作的平行四边形BDEF有没有可能为菱形？若有，请在图乙中作出点E的位置（用尺规作图，并保留作图痕迹）；若没有，请说明理由．

已知,矩形中,,,的垂直平分线分别交、于点、,垂足为.
(1)如图10-1,连接、.求证四边形为菱形,并求的长；
(2)如图10-2,动点、分别从、两点同时出发,沿和各边匀速运动一周.即点自→→→停止,点自→→→停止.在运动过程中,
①已知点的速度为每秒5,点的速度为每秒4,运动时间为秒,当、、、四点为顶点的四边形是平行四边形时,求的值.
②若点、的运动路程分别为、(单位:,),已知、、、四点为顶点的四边形是平行四边形,求与满足的数量关系式.

．用两个全等的等边△ＡＢＣ和△ADC，在平面上拼成菱形ABCD，把一个含60°角的三角尺与这个菱形重合，使三角尺有两边分别在AB、AC上，将三角尺绕点A按逆时针方向旋转


（1）如图1，当三角尺的两边与BC、CD分别相交于点E、F时，
观察或测量BE，CF的长度，你能得出什么结论？
证明你的结论。
图1
（2）如图2，当三角尺的两边与BC、CD的延长线分别交于E、F时，你在（1）中的结论还成立吗？请说明理由。

如图所示，将矩形沿折叠，使点恰好落在上处，以为边作正方形，延长至，使，再以、为边作矩形．

(1). 试比较、的大小，并说明理由．
(2). 令，请问是否为定值？若是，请求出的值；若不是，请说明理由．为定值．
(3). 在（2）的条件下，若为上一点且，抛物线经过、两点，请求出此抛物线的解析式．
(4). 在（3）的条件下，若抛物线与线段交于点，试问在直线上是否存在点，使得以、、为顶点的三角形与相似？若存在，请求直线与轴的交点的坐标；若不存在，请说明理由．

（本题14分）如图，等腰梯形ABCD中，AB=4，CD=9，∠C=60°，动点P从点C出发沿CD方向向点D运动，动点Q同时以相同速度从点D出发沿DA方向向终点A运动，其中一个动点到达端点时，另一个动点也随之停止运动.
（1）求AD的长；
（2）设CP=x， △PDQ的面积为y,求y关于x的函数表达式，并求自变量的取值范围；
（3）探究：在BC边上是否存在点M使得四边形PDQM是菱形？若存在，请找出点M，并求出BM的长；不存在，请说明理由.

如图①，将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD边上的点 M处，点C落在点N处，MN与CD交于点P， 连接EP．
⑴如图②，若M为AD边的中点，①△AEM的周长=_____cm；②求证：EP=AE+DP；

⑵随着落点M在AD边上取遍所有的位置(点M不与A、D重合)，△PDM的周长是否发生变化?请说明理由．

在△ABC中，D为AB边上一点，过点D作DE∥BC交AC于点E，以DE为折线，将△ADE翻折，设所得的△A’DE与梯形DBCE重叠部分的面积为y.
(1)如图(甲)，若∠C=90°，AB=10，BC=6，，则y的值为；
(2)如图(乙)，若AB=AC=10，BC=12，D为AB中点，则y的值为；
(3)若∠B=30°，AB=10，BC=12，设AD=x.
①求y与x的函数解析式；
②y是否有最大值，若有，求出y的最大值；若没有，请说明理由.

图(甲)图(乙)备用图

化简，求值（每题5分）
①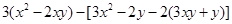
②已知A=3a²+b²-5ab, B=2ab-3b²+4a²,
先求—B+2A，并求当a=-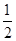, b=2时，—B+2A的值。

（本题6分）已知方程组有两组实数解，，且，，设，
（1）求的取值范围；
（2）用含的代数式表示；（3）是否存在这样的的值，使的值为—2 ？如果存在，求出这样的的值；若不存在，说明理由．

（本题10分）如图直角梯形ABCD中，AD∥BC，AB⊥BC ，AD＝2，AB＝8，CD＝10．
(1)求BC的长；
(2)动点P从点B出发，以1cm/s的速度沿B→A→D方向向点D运动；动点Q从点C出发，以1cm/s的速度沿C→D方向向点D运动；过点Q作QF⊥BC于点F．若P、Q两点同时出发，当其中一点到达终点时整个运动随之结束，设运动时间为t秒．问：在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

(本题10分)已知一次函数y＝的图象与x轴交于点A．与轴交于点；二次函数图象与一次函数y＝的图象交于、两点，与轴交于、两点且的坐标为

（1）求二次函数的解析式；
（2）在轴上是否存在点P，使得△是直角三角形？若存在，求出所有的点，若不存在，请说明理由。

(本题8分)关于x的一元二次方程有两个不相等的实数根．
（1）求k的取值范围．
（2）请选择一个k的负整数值，并求出方程的根．

如图，点在抛物线上，过点作与轴平行的直线交抛物线于点，延长分别与抛物线相交于点，连接，设点的横坐标为，且．

(1).当时，求点的坐标；
(2).当为何值时，四边形的两条对角线互相垂直；
(3).猜想线段与之间的数量关系，并证明你的结论．