观察下列等式 ,
, ,
, ,
,
以上三个等式两边分别相加得:
猜想并写出: 
计算:
(3)探究并计算:
(10分,当总分已达95分时,此题得分不计入总分;当总分不到95分时,计入总分.但计入总分后,总分不得超过95分.)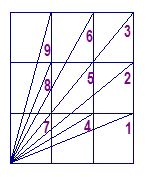
如图为3×3的正方形,求∠1+∠2+∠3+…+∠7+∠8+∠9的和.
﹣(本题12分)已知二次函数y=x2+bx+c与x轴交于A(-1,0)、B(1,0)两点.
(1)求这个二次函数的关系式;
(2)若有一半径为r的⊙P,且圆心P在抛物线上运动,当⊙P与两坐标轴都相切时,求半径r的值.
(3)半径为1的⊙P在抛物线上,当点P的纵坐标在什么范围内取值时,⊙P与y轴相离、相交?
﹣(本题12分)在一平直河岸 同侧有
同侧有 两个村庄,
两个村庄, 到
到 的距离分别是3km和2km,
的距离分别是3km和2km,
 .现计划在河岸
.现计划在河岸 上建一抽水站
上建一抽水站 ,用输水管向两个村庄供水.
,用输水管向两个村庄供水.
方案设计
某班数学兴趣小组设计了两种铺设管道方案:图(1)是方案一的示意图,设该方案中管道长度为 ,且
,且 (其中
(其中 于点
于点 );图(2)是方案二的示意图,设该方案中管道长度为
);图(2)是方案二的示意图,设该方案中管道长度为 ,且
,且 (其中点
(其中点 与点
与点 关于
关于 对称,
对称, 与
与 交于点
交于点 ).
).
 |
(1)观察计算
在方案一中, km(用含
km(用含 的式子表示);
的式子表示);
在方案二中,组长小宇为了计算 的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算,
的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算, km(用含
km(用含 的式子表示).
的式子表示).
(2)探索归纳
①当 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);
当 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”); ②请你参考右边方框中的方法指导,
②请你参考右边方框中的方法指导,
就 (当
(当 时)的所有取值情况进
时)的所有取值情况进
行分析,要使铺设的管道长度较短,
应选择方案一还是方案二?
﹣(本题10分)已知: 如图, AB是⊙O的直径,⊙O过AC的中点D, DE切⊙O于点D, 交BC于点E. 
(1)求证: DE⊥BC;
(2)如果CD=4,CE=3,求⊙O的半径.
如图,在平面直角坐标系 中,抛物线
中,抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与
.所得抛物线与 轴交于
轴交于 两点(点
两点(点 在点
在点 的左边),与
的左边),与 轴交于点
轴交于点 ,顶点为
,顶点为 .
.
(1)求 的值;
的值;
(2)求直线AC的函数解析式。
(3)在线段 上是否存在点
上是否存在点 ,使
,使 与
与 相似.若存在,求出点
相似.若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
如图,抛物线 (
( )与
)与 轴相交于
轴相交于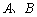 两点,点
两点,点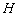 是抛物线的顶点,以
是抛物线的顶点,以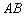 为直径作圆
为直径作圆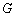 交
交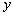 轴于
轴于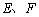 两点,
两点,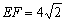 .
.
(1). 用含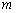 的代数式表示圆
的代数式表示圆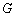 的半径
的半径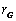 的长;
的长;
)
(2). 连结 ,求线段
,求线段 的长;
的长;
(3). 点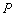 是抛物线对称轴正半轴上的一点,且满足以
是抛物线对称轴正半轴上的一点,且满足以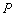 点为圆心的圆
点为圆心的圆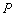 与直线
与直线 和圆
和圆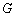 都相切,求点
都相切,求点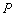 的坐标.
的坐标.
)
如图,在平面直角坐标系xOy中,抛物线 与x轴交于A(1,0)、
与x轴交于A(1,0)、
B(5,0)两点.
(1). 【系统题型:作答题】【阅卷方式:手动】求抛物线的解析式和顶点C的坐标;
(2). 【系统题型:作答题】【阅卷方式:手动】设抛物线的对称轴与x轴交于点D,将∠DCB绕点C按顺时针方向旋转,角的两边CD和CB与x轴分别交于点P、Q,设旋转角为 (0°<
(0°< <90°)
<90°)
①当 等于多少度时,△CPQ是等腰三角形?
等于多少度时,△CPQ是等腰三角形?
②设 ,求s与t之间的函数关系式.
,求s与t之间的函数关系式.

如图,方形ABCD的AB边为直径,在正方形内部作半圆,圆心为O,DF切半圆于点E,交AB的延长线于点F,BF=4.求:
cos∠F的值;BE的长.
如图所示,将矩形 沿
沿 折叠,使点
折叠,使点 恰好落在
恰好落在 上
上 处,以
处,以 为边作正方形
为边作正方形 ,延长
,延长 至
至 ,使
,使 ,再以
,再以 、
、 为边作矩形
为边作矩形 .
.
(1). 试比较 、
、 的大小,并说明理由.
的大小,并说明理由.
2)令 ,请问
,请问 是否为定值?若是,请求出
是否为定值?若是,请求出 的值;若不是,请说明理由.
的值;若不是,请说明理由.
3在(2)的条件下,若 为
为 上一点且
上一点且 ,抛物线
,抛物线 经过
经过 、
、 两点,请求出此抛物线的解析式.
两点,请求出此抛物线的解析式.
(4).在(3)的条件下,若抛物线 与线段
与线段 交于点
交于点 ,试问在直线
,试问在直线 上是否存在点
上是否存在点 ,使得以
,使得以 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似?若存在,请求直线
相似?若存在,请求直线 与
与 轴的交点
轴的交点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知抛物线 与x轴交于不同的两点
与x轴交于不同的两点 和
和 ,与y轴交于点C,且
,与y轴交于点C,且 是方程
是方程 的两个根(
的两个根( ).
).
(1)求抛物线的解析式;
(2)过点A作AD∥CB交抛物线于点D,求四边形ACBD的面积;
(3)如果P是线段AC上的一个动点(不与点A、C重合),过点P作平行于x轴的直线l交BC于点Q,那么在x轴上是否存在点R,使得△PQR为等腰直角三角形?若存在,求出点R的坐标;若不存在,请说明理由.
把两个三角形按如图1放置,其中 ,
,
 ,
,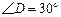 ,且
,且 ,
, .把△DCE
.把△DCE
绕点C顺时针旋转15°得到△D1CE1,如图2,这时AB与
CD1相交于点 ,与D1E1相交于点F.
,与D1E1相交于点F.
(1)求 的度数;
的度数;
(2)求线段AD1的长;
(3)若把△D1CE1绕点 顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.
顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.
如图,在矩形 中,
中, ,
, ,点
,点 从
从 开始沿折线A-B-C-D以4cm/s的速度移动,点
开始沿折线A-B-C-D以4cm/s的速度移动,点 从
从 开始沿
开始沿 边以1cm/s的速度移动,如果点
边以1cm/s的速度移动,如果点 、
、 分别从
分别从 、
、 同时出发,当其中一点到达
同时出发,当其中一点到达 时,另一点也随之停止运动。设运动时间为t(s)。
时,另一点也随之停止运动。设运动时间为t(s)。
⑴t为何值时,四边形 为矩形?
为矩形?
⑵如图10-20,如果 和
和 的半径都是2cm,那么t为何值时,
的半径都是2cm,那么t为何值时, 和
和 外切。
外切。
试题篮
()