初中数学解答题

小平所在的学习小组发现，车辆转弯时，能否顺利通过直角弯道的标图2是某巷子的俯视图，巷子路面宽4 m，转弯处为直角，车辆的车身为矩形ABCD，CD与DE、CE的夹角都是45°时，连接EF，交CD于点G，若GF的长度至少能达到车身宽度，即车辆能通过．
（1）小平认为长8m，宽3m的消防车不能通过该直角转弯，请你帮他说明理由；
为半径的弧），长8m，宽3m的消防车就可以通过该弯道了，具体的方案如图3，其中OM⊥OM′，你能帮小平算出，ON至少为多少时，这种消防车可以通过该巷子，？

（本题6分）如图，四边形是正方形，点在上，，垂足为，请你在上确定一点，使，请你写出两种确定点G的方案，并写出其中一种方案的具体作法和证明．

方案

一： ；

方案

二：（1）作法：

(2) 证明：

如图，在Rt△ABC中，∠C=90°，AC=BC=4cm，点D为AC边上一
点，且AD=3cm，动点E从点A出发，以1cm/s的速度沿线段AB向终点B运动，运动
时间为x s．作∠DEF=45°，与边BC相交于点F．设BF长为ycm．
（1）当x= ▲s时，DE⊥AB；
（2）求在点E运动过程中，y与x之间的函数关系式及点F运动路线的长；
（3）当△BEF为等腰三角形时，求x的值．

操作：小明准备制作棱长为1cm的正方体纸盒，现选用一些废弃的圆形纸片进行如下设计：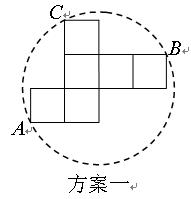


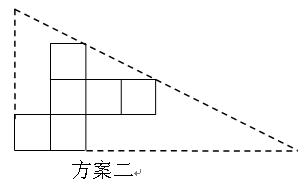
纸片利用率=×100%
发现：（1）方案一中的点A、B恰好为该圆一直径的两个端点．你认为小明的这个发现是否正确，请说明理由．
（2）小明通过计算，发现方案一中纸片的利用率仅约为38.2%．请帮忙计算方案二的利用率，并写出求解过程．
探究：（3）小明感觉上面两个方案的利用率均偏低，又进行了新的设计（方案三），请直
接写出方案三的利用率．

如图，在△ABC中，AB=AC，点O为底边上的中点，以点O为圆心，
1为半径的半圆与边AB相切于点D．
（1）判断直线AC与⊙O的位置关系，并说明理由；
（2）当∠A＝60°时，求图中阴影部分的面积．

已知：抛物线经过坐标原点．
（1）求抛物线的解析式和顶点B的坐标；
（2）设点A是抛物线与轴的另一个交点，试在轴上确定一点P，使PA+PB最短，并求出点P的坐标；
（3）过点A作AC∥BP交轴于点C，求到直线AP、AC、CP距离相等的点的坐标．

已知点A，B分别是两条平行线，上任意两点，C是直线上一点，且
∠ABC=90°，点E在AC的延长线上,BC＝AB (k≠0).
（1）当＝1时，在图（1）中，作∠BEF＝∠ABC，EF交直线于点F.，写出线段EF与
EB的数量关系，并加以证明；
（2）若≠1，如图(2)，∠BEF＝∠ABC，其它条件不变，探究线段EF与EB的数量关系，并说明理由．

已知二次函数的图象经过点，和，反比例
函数（x＞0）的图象经过点（1，2）．
（1）求这两个二次函数的解析式，并在给定的直角坐标系中作出这两个函数的图象；
（2）若反比例函数（）的图象与二次函数）的图象
在第一象限内交于点，落在两个相邻的正整数之间．请你观察图象写出这两个相邻的正整数；
（3）若反比例函数（）的图象与二次函数的
图象在第一象限内的交点为，点的横坐标满足，试求实数的取值范围．

一种电讯信号转发装置的发射直径为31km．现要求：在一边长为30km的正方
形城区选择若干个安装点，每个点安装一个这种转发装置，使这些装置转发的信号能完全
覆盖这个城市．问：
（1）能否找到这样的4个安装点，使得这些点安装了这种转发装置后能达到预设的要求？在图1中画出安装点的示意图，并用大写字母M、N、P、Q表示安装点；
（2）能否找到这样的3个安装点，使得在这些点安装了这种转发装置后能达到预设的要求？在图2中画出示意图说明，并用大写字母M、N、P表示安装点，用计算、推理和文字来说明你的理由．

如图，在中，，是角平分线，平分交于
点，经过两点的交于点，交于点，恰为的直径．

（1）求证：与相切；
（2）当时，求的半径．

在平面直角坐标系中，点坐标为，点坐标为．
（1）如图①，若直线，上有一动点，当点的坐标为　　　　时，有；
（2）如图②，若直线与不平行，在过点的直线上是否存在点，使，若有这样的点，求出它的坐标．若没有，请简要说明理由.

如图,设抛物线C₁:, C₂:,C₁与C₂的交点为A,
B,点A的坐标是,点B的横坐标是－2.
（1）求的值及点B的坐标；
（2）点D在线段AB上,过D作x轴的垂线,垂足为点H,在DH的右侧作正三角形DHG. 过C₂顶点Ｍ的直线记为,且与x轴交于点N.
①若过△DHG的顶点G,点D的坐标为(1, 2)，求点N的横坐标；
②若与△DHG的边DG相交,求点N的横坐标的取值范围.

等腰△ABC，AB=AC=８，∠BAC=120°，P为BC的中点，小亮拿着30⁰角的透明三角板，使30⁰角的顶点落在点P，三角板绕P点旋转．
（1）如图a，当三角板的两边分别交AB、AC于点E、F时．求证：△BPE∽△CFP；
（2）操作：将三角板绕点P旋转到图b情形时，三角板的两边分别交BA的延长线、边AC于点E、F．
①探究１：△BPE与△CFP还相似吗？
②探究２：连结EF，△BPE与△PFE是否相似？请说明理由；
③设EF=m，△EPF的面积为S，试用m的代数式表示S．

如图,已知二次函数y = x－4x + 3的图象交x轴于A、B两点（点A在点B的左侧）抛物线y = x－4x + 3交y轴于点C，
（1）求线段BC所在直线的解析式.
（2）又已知反比例函数与BC有两个交点且k为正整数，求的值.

已知:在△ABC中，BC=a，AC=b，以AB为边作等边三角形ABD. 探究下列问题:
（1）如图1，当点D与点C位于直线AB的两侧时，a=b=3，且∠ACB=60°，则CD=；
（2）如图2，当点D与点C位于直线AB的同侧时，a=b=6，且∠ACB=90°，则CD=；
（3）如图3，当∠ACB变化,且点D与点C位于直线AB的两侧时，求 CD的最大值及相应的∠ACB的度数.

图1图2图3