(25分)如图,在Rt△ABC中,∠B=90°,它的内切圆分别与边BC、CA、AB相切于点D、E、F,联结AD与内切圆相交于另一点P,联结PC、PE、PF.已知PC⊥PF.求证:
(1)EP/DE=PD/DC;(2)△EPD是等腰三角形.
实数x、y、z、w满足x≥y≥z≥w≥0,且5x+4y+3z+6w=100.求x+y+z+w的最大值和最小值.
(本题14分)如图,等腰梯形ABCD中,AB=4,CD=9,∠C=60°,动点P从点C出发沿CD方向向点D运动,动点Q同时以相同速度从点D出发沿DA方向向终点A运动,其中一个动点到达端点时,另一个动点也随之停止运动.
(1)求AD的长;
(2)设CP=x, △PDQ的面积为y,求y关于x的函数表达式,并求自变量的取值范围; (3)探究:在BC边上是否存在点M使得四边形PDQM是菱形?若存在,请找出点M,并求出BM的长;不存在,请说明理由.
(3)探究:在BC边上是否存在点M使得四边形PDQM是菱形?若存在,请找出点M,并求出BM的长;不存在,请说明理由.
课题学习(本题10分)
●探究 (1) 在图1中,已知线段AB,CD,其中点分别为E,F.
①若A (-1,0), B (3,0),则E点坐标为__________;
②若C (-2,2), D (-2,-1),则F点坐标为__________;
(2)在图2中,已知线段AB的端点坐标为A(a,b) ,B(c,d),求出图中AB中点D的坐标(用含a,b,c,d的代数式表示),并给出求解过程.
●归纳无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(a,b),B(c,d), AB中点为D( x,y) 时,x=_________,y=___________.(不必证明)
x,y) 时,x=_________,y=___________.(不必证明)
★●运用在图2中,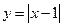 的图象x轴交于P点。一次函数
的图象x轴交于P点。一次函数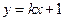 与
与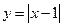 的图象交点为A,B.
的图象交点为A,B.
① 求出交点A
求出交点A ,B的坐标(用k表示);
,B的坐标(用k表示);
②若D为AB中点,且PD垂直于AB时,请利用上面的结论求出k的值。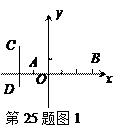
试题篮
()