小明遇到这样一个问题:如图1,在边长为 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)请回答:
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为;
(2)求正方形MNPQ的面积。参考小明思考问题的方法,解决问题:
(3)如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若 ,则AD的长为。
,则AD的长为。
某中学新建了一栋四层的教学楼,每层楼有10间教室,进出这栋教学楼共有4个门,其中两个正门大小相同,两个侧门大小也相同.安全检查中,对4个门进行了测试,当同时开启一个正门和两个侧门时,2分钟内可以通过560名学生;当同时开启一个正门和一个侧门时,4分钟内可以通过800名学生.
(1)求平均每分钟一个正门和一个侧门各可以通过多少名学生?
(2)检查中发现,出现紧急情况时,因学生拥挤,出门的效率将降低20%,安全检查规定:在紧急情况下全楼的学生应在5分钟内通过这4个门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问:该教学楼建造的这4个门是否符合安全规定?请说明理由.
如图①、②、③是两个半径都等于2的⊙O1和⊙O2,由重合状态沿水平方向运动到互相外切过程中的三个位置,⊙O1和⊙O2相交于A、B两点,分别连结O1A、O1B、O2A、O2B和AB。
(1)如图②,当∠AO1B=120°时,求两圆重叠部分图形的周长l;
(2)设∠AO1B的度数为x,两圆重叠部分图形的周长为y,求y关于x的函数关系式,并写出自变量x的取值范围;
(3)在(2)中,当重叠部分图形的周长 时,则线段O2A所在的直线与⊙O1有何位置关系?请说明理由.除此之外,它们是否还有其它的位置关系?如果有,请直接写出其它位置关系时的x的取值范围.
时,则线段O2A所在的直线与⊙O1有何位置关系?请说明理由.除此之外,它们是否还有其它的位置关系?如果有,请直接写出其它位置关系时的x的取值范围.
如图,在平面直角坐标系中,直线y= x+1分别与两坐标轴交于B,A两点,C为该直线上的一动点,以每秒1个单位长度的速度从点A开始沿直线BA向上移动,作等边△CDE,点D和点E都在x轴上,以点C为顶点的抛物线y=a(x﹣m)2+n经过点E.⊙M与x轴、直线AB都相切,其半径为3(1﹣
x+1分别与两坐标轴交于B,A两点,C为该直线上的一动点,以每秒1个单位长度的速度从点A开始沿直线BA向上移动,作等边△CDE,点D和点E都在x轴上,以点C为顶点的抛物线y=a(x﹣m)2+n经过点E.⊙M与x轴、直线AB都相切,其半径为3(1﹣ )a.
)a.
(1)求点A的坐标和∠ABO的度数;
(2)当点C与点A重合时,求a的值;
(3)点C移动多少秒时,等边△CDE的边CE第一次与⊙M相切?
等腰Rt△ABC中,∠BAC=90°,点A、点B分别是x轴、y轴两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E。
(1)如图(1),若A(0,1),B(2,0),求C点的坐标;
(2)如图(2), 当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE;
(3)如图(3),在等腰Rt△ABC不断运动的过程中,若满足BD始终是∠ABC的平分线,试探究:线段OA、OD、BD三者之间是否存在某一固定的数量关系,并说明理由。


已知,如图,在平面直角坐标系中,点A坐标为(-2,0),点B坐标为 (0,2 ),点E为线段AB上的动点(点E不与点A,B重合),以E为顶点作∠OET=45°,射线ET交线段OB于点F,C为y轴正半轴上一点,且OC=AB,抛物线y= x2+mx+n的图象经过A,C两点.
x2+mx+n的图象经过A,C两点.
(1) 求此抛物线的函数表达式;
(2) 求证:∠BEF=∠AOE;
(3) 当△EOF为等腰三角形时,求此时点E的坐标;
(4) 在(3)的条件下,当直线EF交x轴于点D,P为(1) 中抛物线上一动点,直线PE交x轴于点G,在直线EF上方的抛物线上是否存在一点P,使得△EPF的面积是△EDG面积的( ) 倍.若存在,请直接写出点P的坐标;若不存在,请说明理由.
) 倍.若存在,请直接写出点P的坐标;若不存在,请说明理由.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.
如图1,在正方形 中,点
中,点 分别为边
分别为边 的中点,
的中点, 相交于点
相交于点 ,则可得结论:①
,则可得结论:① ;②
;② .(不需要证明)
.(不需要证明)
(1)如图2,若点 不是正方形
不是正方形 的边
的边 的中点,但满足
的中点,但满足 ,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
(2)如图3,若点 分别在正方形
分别在正方形 的边
的边 的延长线和
的延长线和 的延长线上,且
的延长线上,且 ,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
(3)如图4,在(2)的基础上,连接 和
和 ,若点
,若点 分别为
分别为 的中点,请判断四边形
的中点,请判断四边形 是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
四边形 中,
中, ∥
∥ ,
, ,
, ,
, .点
.点 为射线
为射线 上动点(不与点
上动点(不与点 、
、 重合),点
重合),点 在直线
在直线 上,且
上,且 .记
.记 ,
, ,
, ,
, .
.
(1)当点 在线段
在线段 上时,写出并证明
上时,写出并证明 与
与 的数量关系;
的数量关系;
(2)随着点 的运动,(1)中得到的关于
的运动,(1)中得到的关于 与
与 的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的
的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的 的取值范围;
的取值范围;
(3)若cos =
= ,试用
,试用 的代数式表示
的代数式表示 .
.
已知直线 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,将三角形
,将三角形 绕点
绕点 顺时针旋转90°,使点
顺时针旋转90°,使点 落在点
落在点 ,点
,点 落在点
落在点 ,抛物线
,抛物线 过点
过点 、
、 、
、 ,其对称轴与直线
,其对称轴与直线 交于点
交于点 .
.
(1)求抛物线的表达式;
(2)求 的正切值;
的正切值;
(3)点 在
在 轴上,且△
轴上,且△ 与△
与△ 相似,求点
相似,求点 的坐标.
的坐标.
在 中,
中, ,
, ,
, ,⊙
,⊙ 的半径长为1,⊙
的半径长为1,⊙ 交边
交边 于点
于点 ,
,
点 是边
是边 上的动点.
上的动点.
(1)如图1,将⊙ 绕点
绕点 旋转
旋转 得到⊙
得到⊙ ,请判断⊙
,请判断⊙ 与直线
与直线 的位置关系;
的位置关系;
(2)如图2,在(1)的条件下,当 是等腰三角形时,求
是等腰三角形时,求 的长;
的长;
(3)如图3,点 是边
是边 上的动点,如果以
上的动点,如果以 为半径的⊙
为半径的⊙ 和以
和以 为半径的⊙
为半径的⊙ 外切,设
外切,设 ,
, ,求
,求 关于
关于 的函数关系式及定义域..
的函数关系式及定义域..
如图,⊙ 的半径为6,线段
的半径为6,线段 与⊙
与⊙ 相交于点
相交于点 、
、 ,
, ,
, ,
, 与⊙
与⊙ 相交于点
相交于点 ,设
,设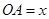 ,
, .
.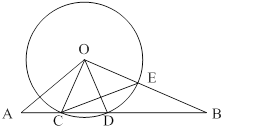
(1)求 长;
长;
(2)求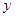 关于
关于 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(3)当 ⊥
⊥ 时,求
时,求 的长.
的长.
已知, ,
,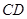 是
是 的平分线,点
的平分线,点 在
在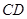 上,
上, .将三角板的直角顶点放置在点
.将三角板的直角顶点放置在点 处,绕着点
处,绕着点 旋转,三角板的一条直角边与射线
旋转,三角板的一条直角边与射线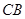 交于点
交于点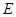 ,另一条直角边与直线
,另一条直角边与直线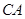 、直线分别交于点
、直线分别交于点 、点
、点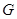 .
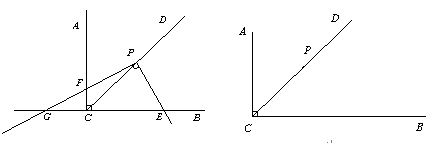
.
(1)如图,当点 在射线
在射线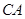 上时,
上时,
①求证: 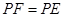 ;
;
②设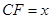 ,
,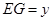 ,求
,求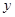 与
与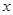 的函数解析式并写出函数的定义域;
的函数解析式并写出函数的定义域;
(2)连结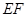 ,当△
,当△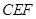 与△
与△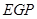 似时,求
似时,求 的长.
的长.
十一届全国人大常委会第二十次会议审议的个人所得税法修正案草案(简称“个税法草案”),拟将现行个人所得税的起征点由每月2000元提高到3000元,并将9级超额累进税率修改为7级,两种征税方法的1~5级税率情况见下表:
| 税 级 |
现行征税方法 |
草案征税方法 |
||||
| 月应纳税额x |
税率 |
速算扣除数 |
月应纳税额x |
税率 |
速算扣除数 |
|
| 1 |
x ≤ 500 |
5% |
0 |
x ≤ 1 500 |
5% |
0 |
| 2 |
500<x≤2 000 |
10% |
25 |
1 500<x≤4 500 |
10% |
▲ |
| 3 |
2 000<x≤5 000 |
15% |
125 |
4 500<x≤9 000 |
20% |
▲ |
| 4 |
5 000<x≤20 000 |
20% |
375 |
9 000<x≤35 000 |
25% |
975 |
| 5 |
20 000<x≤40 000 |
25% |
1375 |
35 000<x≤55 000 |
30% |
2 725 |
注:“月应纳税额”为个人每月收入中超出起征点应该纳税部分的金额。
“速算扣除数”是为了快捷简便计算个人所得税而设定的一个数。
例如:按现行个人所得税法的规定,某人今年3月的应纳税额为2 600元,他应缴税款可以用下面两种方法之一来计算:
方法一:按1~3级超额累进税率计算,即500×5% + 1500×10% + 600×15% =
265(元)
方法二:用“月应纳税额×适用税率−速算扣除数”计算,即2600×15% − 125 =
265(元)
(1)请把表中空缺的“速算扣除数”填写完整;
(2)甲今年3月缴了个人所得税1 060元,若按“个税法草案”计算,则他应缴税
款多少元?
(3)乙今年3月缴了个人所得税3千多元,若按“个税法草案”计算,他应缴纳的
税款恰好不变,那么乙今年3月所缴税款的具体数额为多少元?
如图,矩形ABCD中,AB=8,AD=10.
(1)求矩形ABCD的周长;
(2)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.
①求DE的长;
②点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长.
(3)M是AD上的动点,在DC 上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处, 求线段CT长度的最大值与最小值之和。
试题篮
()