初中数学解答题

请用直尺、圆规作图，不写作法，但要保留作图痕迹．

已知：，直线及上两点，．

求作：，使点在直线的上方，且，．

如图，在正方形中，是边上一点，（与、不重合），连接，将沿所在的直线折叠得到，延长交于，连接，作，与的延长线交于点，连接．显然是的平分线，是的平分线．仔细观察，请逐一找出图中其他的角平分线（仅限于小于的角平分线），并说明理由．

汛期到来，山洪暴发．下表记录了某水库内水位的变化情况，其中表示时间（单位：，表示水位高度（单位：，当时，达到警戒水位，开始开闸放水．

	0	2	4	6	8	10	12	14	16	18	20
	14	15	16	17	18	14.4	12	10.3	9	8	7.2

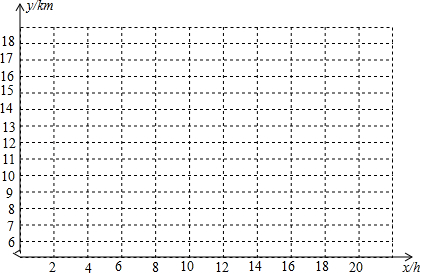
（1）在给出的平面直角坐标系中，根据表格中的数据描出相应的点．

（2）请分别求出开闸放水前和放水后最符合表中数据的函数解析式．

（3）据估计，开闸放水后，水位的这种变化规律还会持续一段时间，预测何时水位达到．

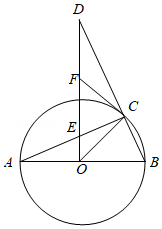
如图，是的直径，是上一点，过点作，交的延长线于，交于点，是的中点，连接．

（1）求证：是的切线．

（2）若，求证：．

鲁南高铁临沂段修建过程中需要经过一座小山．如图，施工方计划沿方向开挖隧道，为了加快施工速度，要在小山的另一侧、、共线）处同时施工．测得，，，求的长．

争创全国文明城市，从我做起，某学校在七年级开设了文明礼仪校本课程，为了解学生的学习情况，学校随机抽取30名学生进行测试，成绩如下（单位：分）

78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93

整理上面的数据得到频数分布表和频数分布直方图：

成绩（分	频数
	5
	11
	2

回答下列问题：

（1）以上30个数据中，中位数是　　；频数分布表中　　；　　；

（2）补全频数分布直方图；

（3）若成绩不低于86分为优秀，估计该校七年级300名学生中，达到优秀等级的人数．

解方程：．

如图，内接于，为直径，作交于点，延长，交于点，过点作的切线，交于点．

（1）求证：；

（2）如果，，求弦的长．

如图，点，，是直线与反比例函数图象的两个交点，轴，垂足为点，已知，连接，，．

（1）求直线的表达式；

（2）和的面积分别为，．求．

某数学兴趣小组要测量实验大楼部分楼体的高度（如图①所示，部分），在起点处测得大楼部分楼体的顶端点的仰角为，底端点的仰角为，在同一剖面沿水平地面向前走20米到达处，测得顶端的仰角为（如图②所示），求大楼部分楼体的高度约为多少米？（精确到1米）

（参考数据：，，，，

在菱形中，点是边上一点，连接，点，是上的两点，连接，，使得，．

求证：（1）；

（2）．

某商场的运动服装专柜，对，两种品牌的运动服分两次采购试销后，效益可观，计划继续采购进行销售．已知这两种服装过去两次的进货情况如下表：

	第一次	第二次
品牌运动服装数件	20	30
品牌运动服装数件	30	40
累计采购款元	10200	14400

（1）问，两种品牌运动服的进货单价各是多少元？

（2）由于品牌运动服的销量明显好于品牌，商家决定采购品牌的件数比品牌件数的倍多5件，在采购总价不超过21300元的情况下，最多能购进多少件品牌运动服？

学习一定要讲究方法，比如有效的预习可大幅提高听课效率．九年级（1）班学习兴趣小组为了了解全校九年级学生的预习情况，对该校九年级学生每天的课前预习时间（单位：进行了抽样调查，并将抽查得到的数据分成5组，下面是未完成的频数、频率分布表和频数分布扇形图：

组别	课前预习时间	频数（人数）	频率
1		2
2			0.10
3		16	0.32
4
5		3

请根据图表中的信息，回答下列问题：

（1）本次调查的样本容量为　　，表中的　　，　　，　　；

（2）试计算第4组人数所对应的扇形圆心角的度数；

（3）该校九年级共有1000名学生，请估计这些学生中每天课前预习时间不少于的学生人数．

计算：．

阅读下面的材料：

如果函数满足：对于自变量的取值范围内的任意，，

（1）若，都有，则称是增函数；

（2）若，都有，则称是减函数．

例题：证明函数是减函数．

证明：设，

．

，

，．

．即．

．

函数是减函数．

根据以上材料，解答下面的问题：

已知函数，

，

（1）计算：　　，　　；

（2）猜想：函数是　　函数（填“增”或“减” ；

（3）请仿照例题证明你的猜想．