在中,
,
,
于点
.

(1)如图1,点,
分别在
,
上,且
,当
,
时,求线段
的长;
(2)如图2,点,
分别在
,
上,且
,求证:
;
(3)如图3,点在
的延长线上,点
在
上,且
,求证:
.
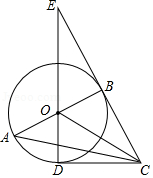
如图,在中,
,以
为直径作
,点
为
上一点,且
,连接
并延长交
的延长线于点
.
(1)判断直线与
的位置关系,并说明理由;
(2)若,
,求圆的半径及
的长.
4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读,该校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
一、数据收集,从全校随机抽取20学生,进行每周用于课外阅读时间的调查,数据如下(单位:
30 |
60 |
81 |
50 |
44 |
110 |
130 |
146 |
80 |
100 |
60 |
80 |
120 |
140 |
75 |
81 |
10 |
30 |
81 |
92 |
二、整理数据,按如下分段整理样本数据并补全表格:
课外阅读时间 |
||||
等级 |
||||
人数 |
3 |
8 |
三、分析数据,补全下列表格中的统计量:
平均数 |
中位数 |
众数 |
80 |
81 |
四、得出结论:
①表格中的数据: ,
,
;
②用样本中的统计量估计该校学生每周用于课外阅读时间的等级为 ;
③如果该校现有学生400人,估计等级为“”的学生有 人;
④假设平均阅读一本课外书的时间为320分钟,请你用样本平均数估计该校学生每人一年(按52周计算)平均阅读 本课外书.
如图,是菱形
的对角线,
,
(1)请用尺规作图法,作的垂直平分线
,垂足为
,交
于
;(不要求写作法,保留作图痕迹)
(2)在(1)条件下,连接,求
的度数.

[问题探究]
(1)如图1,和
均为等腰直角三角形,
,点
,
,
在同一直线上,连接
,
.
①请探究与
之间的位置关系: ;
②若,
,则线段
的长为 ;
[拓展延伸]
(2)如图2,和
均为直角三角形,
,
,
,
,
.将
绕点
在平面内顺时针旋转,设旋转角
为
,作直线
,连接
,当点
,
,
在同一直线上时,画出图形,并求线段
的长.

如图所示,一种适用于笔记本电脑的铝合金支架,边,
可绕点
开合,在
边上有一固定点
,支柱
可绕点
转动,边
上有六个卡孔,其中离点
最近的卡孔为
,离点
最远的卡孔为
.当支柱端点
放入不同卡孔内,支架的倾斜角发生变化.将电脑放在支架上,电脑台面的角度可达到六档调节,这样更有利于工作和身体健康,现测得
的长为
,
为
,支柱
为
.
(1)当支柱的端点放在卡孔
处时,求
的度数;
(2)当支柱的端点放在卡孔
处时,
,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)
参考数据表
计算器按键顺序 |
计算结果(已取近似值) |
|
2.65 |
|
6.8 |
|
11.24 |
|
0.35 |
|
0.937 |
|
41 |
|
49 |
|
49 |
|
41 |

如图,在矩形中,
,
,点
在
上,将
沿
折叠,点
恰好落在对角线
上的
点,
为
上一点,
经过点
,
(1)求证:是
的切线;
(2)在边上截取
,点
是线段
的黄金分割点吗?请说明理由.

亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
十八大以来,某校已举办五届校园艺术节,为了弘扬中华优秀传统文化,每届艺术节上都有一些班级表演“经典诵读”“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计,并绘制了如图所示不完整的折线统计图和扇形统计图.

(1)五届艺术节共有 个班级表演这些节目,班数的中位数为 ,在扇形统计图中,第四届班级数的扇形圆心角的度数为 ;
(2)补全折线统计图;
(3)第六届艺术节,某班决定从这四项艺术形式中任选两项表演 “经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用
,
,
,
表示),利用树状图或表格求出该班选择
和
两项的概率.
试题篮
()