如图,已知二次函数图象的顶点坐标为,与坐标轴交于
、
、
三点,且
点的坐标为
.
(1)求二次函数的解析式;
(2)在二次函数图象位于轴上方部分有两个动点
、
,且点
在点
的左侧,过
、
作
轴的垂线交
轴于点
、
两点,当四边形
为矩形时,求该矩形周长的最大值;
(3)当矩形的周长最大时,能否在二次函数图象上找到一点
,使
的面积是矩形
面积的
?若存在,求出该点的横坐标;若不存在,请说明理由.
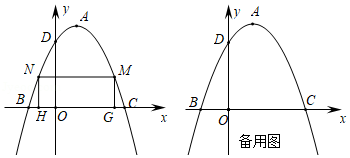
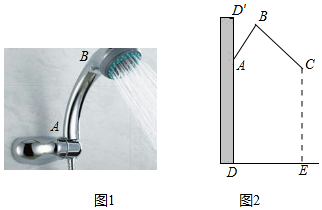
图1是一种淋浴喷头,图2是图1的示意图,若用支架把喷头固定在点处,手柄长
,
与墙壁
的夹角
,喷出的水流
与
形成的夹角
,现在住户要求:当人站在
处淋浴时,水流正好喷洒在人体的
处,且使
,
.问:安装师傅应将支架固定在离地面多高的位置?
(参考数据:,
,
,
,
,
,
,
,
.
为了扎实推进精准扶贫工作,某地出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为、
、
、
类贫困户.为检査帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:

请根据图中信息回答下面的问题:
(1)本次抽样调查了多少户贫困户?
(2)抽查了多少户类贫困户?并补全统计图;
(3)若该地共有13000户贫困户,请估计至少得到4项帮扶措施的大约有多少户?
(4)为更好地做好精准扶贫工作,现准备从类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用树状图或列表法求出恰好选中甲和丁的概率.
某生态体验园推出了甲、乙两种消费卡,设入园次数为时所需费用为
元,选择这两种卡消费时,
与
的函数关系如图所示,解答下列问题
(1)分别求出选择这两种卡消费时,关于
的函数表达式;
(2)请根据入园次数确定选择哪种卡消费比较合算.

如图,一次函数的图象与反比例函数
在第一象限的图象交于
和
两点,与
轴交于点
.
(1)求反比例函数的解析式;
(2)若点在
轴上,且
的面积为5,求点
的坐标.

如图1,正方形和
的边
,
在同一条直线上,且
,取
的中点
,连接
,
,
.
(1)试证明,并求
的值.
(2)如图2,将图1中的正方形变为菱形,设,其它条件不变,问(1)中
的值有变化吗?若有变化,求出该值(用含
的式子表示);若无变化,说明理由.

如图,在中,
,
的平分线
交
于点
,点
在
上,以
为直径的
经过点
.
(1)求证:①是
的切线;
②;
(2)若点是劣弧
的中点,且
,试求阴影部分的面积.

“一带一路”促进了中欧贸易的发展,我市某机电公司生产的,
两种产品在欧洲市场热销.今年第一季度这两种产品的销售总额为2060万元,总利润为1020万元(利润
售价
成本).其每件产品的成本和售价信息如下表:
成本(单位:万元 |
2 |
4 |
售价(单位:万元 |
5 |
7 |
问该公司这两种产品的销售件数分别是多少?
文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 |
年龄段 |
频数(人数) |
第1组 |
5 |
|
第2组 |
||
第3组 |
35 |
|
第4组 |
20 |
|
第5组 |
15 |

(1)请直接写出 ,
,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有岁的市民300万人,问
岁年龄段的关注本次大会的人数约有多少?
试题篮
()