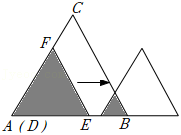
如图,等边 、等边 的边长分别为 和 .开始时点 与点 重合, 在 上, 在 上, 沿 向右平移,当点 到达点 时停止.在此过程中,设 重合部分的面积为 , 移动的距离为 ,则 与 的函数图象大致为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
为了增强学生的安全防范意识,某校初三(1)班班委举行了一次安全知识抢答赛,抢答题一共 个,记分规则如下:每答对一个得 分,每答错或不答一个扣 分.小红一共得 分,则小红答对的个数为( )
| A. |
|
B. |
|
C. |
|
D. |
|
在一个不透明的布袋内,有红球 个,黄球 个,白球 个,蓝球 个,它们除颜色外,大小、质地都相同.若随机从袋中摸取一个球,则摸中哪种球的概率最大( )
| A. |
红球 |
B. |
黄球 |
C. |
白球 |
D. |
蓝球 |
2022年4月18日,国家统计局发布数据,今年一季度国内生产总值 亿元.同比增长 ,比2021年四季度环比增长 .把 用科学记数法表示为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
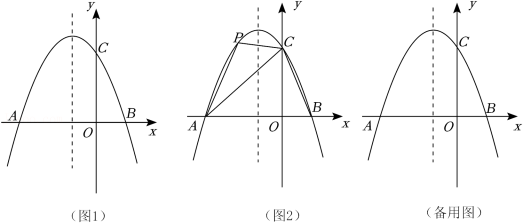
如图1,平面直角坐标系 中,抛物线 与 轴分别交于点 和点 ,与 轴交于点 ,对称轴为直线 ,且 , 为抛物线上一动点.
(1)直接写出抛物线的解析式;
(2)如图2,连接 ,当点 在直线 上方时,求四边形 面积的最大值,并求出此时 点的坐标;
(3)设M为抛物线对称轴上一动点,当 运动时,在坐标轴上是否存在点 ,使四边形 为矩形?若存在,直接写出点 及其对应点 的坐标;若不存在,请说明理由.
《几何原本》是古希腊数学家欧几里得的一部不朽著作,是数学发展史的一个里程碑.在该书的第2卷“几何与代数”部分,记载了很多利用几何图形来论证的代数结论,利用几何给人以强烈印象将抽象的逻辑规律体现在具体的图形之中.
(1)我们在学习许多代数公式时,可以用几何图形来推理,观察下列图形,找出可以推出的代数公式,(下面各图形均满足推导各公式的条件,只需填写对应公式的序号)

公式①:
公式②:
公式③:
公式④:
图1对应公式_____,图2对应公式_____,图3对应公式_____,图4对应公式_____.
(2)《几何原本》中记载了一种利用几何图形证明平方差公式 的方法,如图5,请写出证明过程;(已知图中各四边形均为矩形)
(3)如图6,在等腰直角三角形 中, , 为 的中点, 为边 上任意一点(不与端点重合),过点 作 于点 ,作 于点 ,过点 作 交 的延长线于点 .记 与 的面积之和为 , 与 的面积之和为 .
①若 为边 的中点,则 的值为_____;
②若 不为边 的中点时,试问①中的结论是否仍成立?若成立,写出证明过程;若不成立,请说明理由.

试题篮
()