质量为60kg的小明站在水平地面上,利用如图甲所示装置提升物体A。物体A的质量mA为74kg,底面积SA为2×10-2m2。当小明施加竖直向下的拉力为F1时,物体A未被拉动,此时物体A对地面的压强p为5×103Pa,小明对地面的压强为p1;当小明施加竖直向下的拉力为F2时,物体A恰好匀速上升,拉力F2做的功随时间变化的图象如图乙所示。小明对地面的压强为p2,且p1:p2="16:" 15。已知B、C、D、E四个滑轮的质量相同,不计绳重和摩擦,g取10N/kg。求:
(1)当小明施加竖直向下的拉力F1时,物体A对地面的压力FN;
(2)每个滑轮所受的重力G0;
(3)小明施加竖直向下的拉力F2时,物体上升的速度。
建筑工人使用如图所示装置,将质量分布均匀的长方体水泥板M吊起后放入水中。工人通过控制电动机A、电动机B,始终保持水泥板M所受拉力竖直向上。当电动机A对绳的拉力为零时,电动机A对地面的压强为p0;当水泥板M一端被竖直滑轮组拉起,另一端仍停在地面上,且水泥板M与水平地面成某角度时,电动机A对地面的压强为p1;当水泥板M被竖直滑轮组拉离地面时,电动机A对地面的压强为p2;当将水泥板M被悬挂着浸没在水中时,电动机A对地面的压强为p3。已知:水泥板M的体积VM为0.1m3, =
= =5250Pa,
=5250Pa, =
= =10250Pa,
=10250Pa, =
= =5250Pa,不计绳重和轴摩擦。(g取10N/kg)求:
=5250Pa,不计绳重和轴摩擦。(g取10N/kg)求:
(1)竖直滑轮组中动滑轮的总重力G动 ;
(2)水泥板M所受重力GM;
(3)竖直滑轮组提拉水泥板M将其立起的过程中机械效率η。(结果保留两位有效数字)
如图所示,是使用汽车打捞水下重物的示意图。汽车通过滑轮组打捞水下一个圆柱形重物,在整个打捞过程中,汽车以0.3m/s的速度向右水平匀速运动。重物在水面下被提升的过程共用时50s,汽车拉动绳子的功率P1为480W。重物开始露出水面到完全被打捞出水的过程共用时10s,此过程中汽车拉动绳子的功率逐渐变大,当重物完全被打捞出水后,汽车的功率P2比P1增加了120W,且滑轮组机械效率为80%。忽略水的阻力、绳重和滑轮的摩擦,g取10N/kg。求: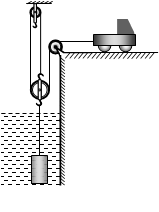
(1)重物浸没在水中所受浮力;
(2)打捞前重物上表面受到水的压力;
(3)被打捞重物的密度
用如图(1)所示的装置提升重物,水平横梁AB 固定在支架C顶端,OA: OB=4:1。横梁A端挂一底面积为S=0.1m2的配重M,横梁B端下挂着由质量相等的四个滑轮组成的滑轮组,用此滑轮组多次提升不同的物体,计算出滑轮组的机械效率,并记入下面的表格。
| 物重G/N |
60 |
80 |
100 |
180 |
| 机械效率η |
0.75 |
0.80 |
0.833 |
0. 90 |

现用滑轮组分别提升甲、乙两个物体:在水面以上提升密度为ρ甲=0.75kg/dm3的甲物体时,绳自由端的拉力为F1,F1做的功为W1,配重M对地面的压强变化量为ΔP1;在水面以下提升密度为ρ乙=5.6kg/dm3的乙物体时,绳自由端的拉力为F2,F2做的功为W2,配重M对地面的压强变化量ΔP2。
F1、F2所做的功随时间变化的关系如图(2)所示。已知:甲、乙两物体的体积关系为V甲=4V乙,提升甲、乙两物体时速度相同。(不计绳的质量、杠杆的质量、轮与轴的摩擦、水对物体的阻力。取g =10N/kg)求:
(1)配重M对地面的压强变化量的差ΔP2-ΔP1
(2)滑轮组提升浸没在水中的乙物体时的机械效率。(保留百分号前面一位小数)
如图所示为一种蓄水箱的放水装置,AOB是以O点为转轴的轻质杠杆,AO呈水平状态,如图A、O两点间距离为40cm, B、O两点间距离为20cm,且OB与水平面夹角为60°。A点正下方的Q是一个轻质、横截面积为100cm2的盖板(盖板恰好能堵住出水口),它通过细绳与杠杆的A端相连。在水箱右侧的水平工作台上,有一质量为60kg的人通过滑轮组拉动系在B点呈竖直状态的绳子,从而可以控制水是否能从出水口流出。若水箱中水深为50cm,当盖板恰好要被拉起时,人对绳子的拉力为F1,工作台对人的支持力为N1;若水箱中水深为100cm,当盖板恰好要被拉起时,人对绳子的拉力为F2,工作台对人的支持力为N2。已知N1与N2之比为9:7,盖板的厚度、绳重及滑轮的摩擦均可忽略不计,人对绳的拉力与人所受重力在同一直线上,取g=10N/kg。求:
(1)动滑轮所受的重力
(2)F1:F2
(3)当水位至少达到多高时,人无法拉起盖板。
如图甲所示,正方体A边长0.2m,作为配重使用,杠杆OE:OF=2:3,某同学用这个装置和一个密闭容器D提取水中的圆柱体B, 圆柱体B的体积是密闭容器D的 ;旁边浮体C的体积是0.1m3,该同学站在浮体C上,总体积的
;旁边浮体C的体积是0.1m3,该同学站在浮体C上,总体积的 浸入水中;该同学用力拉动滑轮组绕绳自由端,手拉绳的功率P和密闭容器D匀速被提升的距离关系如图24乙所示;密闭容器D上升速度0.05m/s保持不变,密闭容器D被提出水后,圆柱体B从密闭容器D中取出放在浮体C的上面,同时手松开绳子时,浮体C露出水面的体积减少总体积的
浸入水中;该同学用力拉动滑轮组绕绳自由端,手拉绳的功率P和密闭容器D匀速被提升的距离关系如图24乙所示;密闭容器D上升速度0.05m/s保持不变,密闭容器D被提出水后,圆柱体B从密闭容器D中取出放在浮体C的上面,同时手松开绳子时,浮体C露出水面的体积减少总体积的 ;在提升全过程中,配重A始终没有离开地面。两个定滑轮总重10 N.(绳的重力,滑轮与轴的摩擦及水的阻力不计。g=10N/kg),求:
;在提升全过程中,配重A始终没有离开地面。两个定滑轮总重10 N.(绳的重力,滑轮与轴的摩擦及水的阻力不计。g=10N/kg),求: (1)圆柱体B的重力;
(1)圆柱体B的重力;
(2)密闭容器D离开水面时,滑轮组提升重物B的机械效率;(百分号前面保留整数);
(3)圆柱体B的密度;
(4)在提升全过程中配重A对地面的压强的最大变化量。
如图是利用电子秤显示水库水位装置的示意图。该装置主要由不计重力的滑轮C、D,长方体物块A、B以及轻质杠杆MN组成。物块A通过细绳与滑轮C相连,物块B通过细绳与杠杆相连。杠杆可以绕支点O在竖直平面内转动,杠杆始终在水平位置平衡,且MO:ON=1:2。已知物块A的密度为1.5×103kg/m3,底面积为0.04m2,高1 m,物块B的重力为100N。滑轮与转轴的摩擦、杠杆与轴的摩擦均忽略不计,求:

(1)当物块A的顶部刚没入水面时,底部受到水的压强大小;
(2)当物块A的顶部刚没入水面时,物块A所受的拉力大小;
|
(3)若水位发生变化,当电子秤的示数为40 N时,求物块A浸入水中的深度。
小明同学设计的“风力测试仪”在校科技节上备受师生们的青睐,“风力测试仪”的原理如图所示.电源电压6V,R0为保护电阻,AB为长20cm、阻值为50W的均匀电阻丝.OP为质量、电阻均不计的金属细杆,下端连接一个重为2N的球P.闭合开关S,无风时,OP下垂并与电阻丝的B端接触;有风时,球P受风力的作用,使金属细杆OP绕悬挂点O偏转,当偏转到电阻丝的A端时,电流表示数为0.6A.已知悬挂点O与电阻丝B端的距离为10cm,金属细杆OP始终与电阻丝AB接触良好且无摩擦, 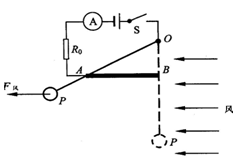
求:(1) R0的阻值;
(2)无风时电流表示数;
(3)在风力作用下,当金属细杆OP在图示位置静止时,作出F风的力臂,并求出该力的大小.
如图是锅炉安全阀示意图、阀的横截面积S为4厘米2,OA∶AB=1∶2,若锅炉能承受的最大压强为5.4×105帕,在B处应挂多重的物体G?若锅炉能承受的最大压强减小,为保证锅炉的安全,应将重物向什么方向移动? 
电气化铁路的高压输电线,无论在严冬还是盛夏都要绷直,才能使高压线与列车的电极接触良好,这就必须对高压线施加恒定的拉力。为此,工程师设计了如图所示的恒拉力系统,其简化原理图如图所示。实际测量得到每个水泥块的体积为1.5×10-2m3,共悬挂20个水泥块。已知水泥块的密度为2.6×103kg/m3,g取10N/kg。
(1)请指出图中的动滑轮、定滑轮;
(2)每个水泥块的重力是多少?
(3)滑轮组对高压线的拉力是多大?
 |
|||
 |
|||
示轻质杠杆,把密度均为4.0×103kg/m3的甲、乙两个实心物体挂在A、B两端时,杠杆在水平位置平衡,若将甲物体浸没在水中,同时把支点从O移到O′时,杠杆又在新的位置平衡,若两次支点的距离O O′为OA的 ,求:甲、乙两个物体的质量之比.
,求:甲、乙两个物体的质量之比.
图1—5—19
图是某课外科技小组的同学设计的厕所自动冲水装置的示意图,它在自来水管持续供给的较小量的水储备到一定量后,自动开启放水阀门,冲洗厕所.实心圆柱体浮体A的质量为5.6kg,高为0.18m,阀门B的面积为7.5×10﹣3m2;连接A、B的是体积和质量都不计的硬杆,长为0.16m.当浮体A露出水面的高度只有0.02m时,阀门B恰好被打开,水箱中的水通过排水管开始排出.已知水的密度为1×103kg/m3,不计阀门B的质量和厚度.当水箱开始排水时,求:
(1)浮体A受到的重力;
(2)水对阀门B的压强和压力;
(3)浮体A受到的浮力;
(4)浮体A的密度.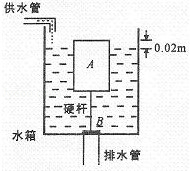
我国是世界上第一个成功完成海底沉船整体打捞工作的国家,图甲是起重工程船将“南海1号”沉船打捞出水的情况.为分析打捞工作,我们可以将实际打捞过程简化为如图乙所示的滑轮组竖直向上提升水中的金属物.已知正方体实心金属物的体积V=1×10-2m3,密度ρ金=7.9×103kg/m3,ρ水=1×103kg/m3,g=10N/kg,绳子重力不计.请问: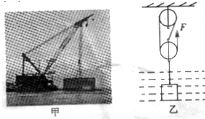
(1)若不计摩擦和滑轮重,当金属物始终浸没在水中时,需要多大的竖直向上拉力作用于绳子自由端才能将金属物匀速提升?
(2)若仍不计摩擦,但动滑轮重G0=60N,要求在1min内将始终浸没在水中的金属物匀速提升6m,求绳子自由端竖直向上拉力的功率;
(3)若将金属物完全提出水面后继续向上匀速提升的过程中,该滑轮组的机械效率为94%,问作用于绳子自由端竖直向上的拉力是多大?(计算结果保留整数)
如图所示,是我校物理兴趣活动小组设计的一个健身器材,它是由一个质量为m1长为2L的木棒和一个质量为m2半径为R 的球体组成,同学们在活动中利用所学物理知识找出了该器材的重心。你能确定重心点O到A端的距离L0吗?请推导并写出L0与已知量的关系式。
如图所示,某科技小组的同学制作了一个打捞物体的自动控制模型,E为配重,AOB是一个质地均匀的长方形横杆,其质量不计,OA∶OB=1∶3,在水平位置保持平衡。通过电动机Q可以控制杠杆B端抬起,从而将被打捞物体提起。已知滑轮D重为10N,B端定滑轮和提升电动机P的总质量是1kg,提升电动机P的功率为3W且保持不变,物体M的质量是1kg。只让提升电动机P工作,当物体M匀速上升时,提升电动机P对绳子的拉力为F1, B端滑轮组的机械效率为η1。若用质量为1.5kg物体N代替物体M,只让提升电动机P工作,当物体N匀速上升时,提升电动机P对绳子的拉力为F2, B端滑轮组的机械效率为η2,且η1∶η2=8∶9。不计绳的质量,不计滑轮与轴的摩擦,g取10N/kg,求:
(1)F1与F2的比值;
(2)只让提升电动机P工作,当物体M匀速上升时的速度υ;
(3)当物体N被提升到一定高度后,提升电动机P停止工作,启动电动机Q将杠杆B端匀速抬起的过程中,电动机Q对绳子的拉力F的大小。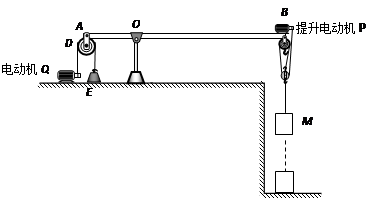
试题篮
()