“蛟龙号”悬停时,上表面深度为7000米,重力为 。
(1)蛟龙号悬停时,求 ;
(2)蛟龙号的 很大,相当于手掌上放一辆 牛的卡车,手掌面积为 ,求 的估值;
(3)推论 ;
(4)已知蛟龙号上表面海水密度随深度增大而增大。设液体压强为 ,海水密度为 ,上表面深度为 ,能不能说明 ,并说明理由。
如图所示,质量为10kg,底面积为500cm 2的圆柱体A放在水平面上。一薄壁圆柱形容器B也置于水平面上,该容器足够高,底面积为200cm 2,内盛有8kg的水。若将一物体M分别放在圆柱体A上表面的中央和浸没在容器B的水中时,圆柱体A对水平面的压强变化量和水对容器B底部压强的变化量相等(g取10N/kg,ρ 水=1.0×10³kg/m³),则( )

| A. |
未放上物体M时,圆柱体A对水平地面的压强为2×10 5Pa |
| B. |
容器B内水的体积为0.08m³ |
| C. |
物体M的密度为2.5×10³kg/m³ |
| D. |
物体M未放入容器B时,容器B底部受到的水的压强为4×10 4Pa |
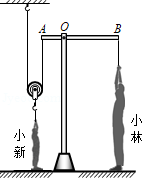
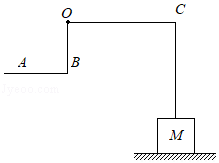
如图所示,站在水平地面上的小林想通过杠杆 和动滑轮拉起同样站在水平地面上的小新。杠杆 可绕转轴 在竖直平面内转动,且 ,小林的质量 。小新的质量 ,小新双脚与地面接触面积 。当小林施加竖直向下的拉力 时,小新未被拉动,此时小新对地面的压强 ,小林对地面的压强为 ;当小林施加竖直向下的拉力 时,小新刚好被拉起,小林对地面的压强为 ,且 。不计绳重,杠杆重力和一切摩擦, 取 。求:
(1)小林施加拉力 时,小新对地面的压力 ;
(2)动滑轮重力 。
如图甲所示,薄壁圆柱形容器放在水平台上,容器的底面积 ,质量均匀的圆柱体物块上表面中央用足够长的细绳系住,悬挂于容器中。以恒定速度向容器中缓慢注水(每分钟注入 ,直至注满容器为止,细绳的拉力大小与注水时间的关系图像如图乙所示。 ,常数 ,物块不吸水,忽略细绳体积、液体扰动等其它次要因素。

(1)求注水前圆柱体物块的下表面到容器底部的距离 ;
(2)当细绳的拉力为 时,求水对物块下表面的压强;
(3)若改为以恒定速度向容器中缓慢注入另一种液体(每分钟注入 , ,直至 时停止。求容器底部所受液体压强 与注液时间 分钟 的函数关系式。
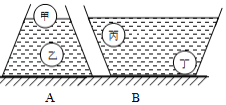
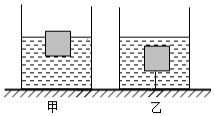
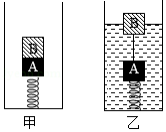
两个底面积相同形状不同的容器  盛有同种液体,放在水平桌面上,液体深度相同,把甲、乙、丙、丁四个体积相同的小球放入两个容器中,小球静止后位置如图所示,两容器内液体深度依旧相同。下列说法正确的是
盛有同种液体,放在水平桌面上,液体深度相同,把甲、乙、丙、丁四个体积相同的小球放入两个容器中,小球静止后位置如图所示,两容器内液体深度依旧相同。下列说法正确的是 

| A. |
甲球密度小于丙球密度 |
| B. |
甲球受到的浮力大于丁球受到的浮力 |
| C. |
取出乙、丙小球后, |
| D. |
取出乙、丙小球后, |
如图所示,弹簧测力计下悬挂着不吸水的圆柱体,圆柱体质量为180g。不计厚度的平底容器置于水平桌面上,质量为100g,底面积为50cm 2,高为8cm,容器内盛有质量为350g的水。当圆柱体浸入水中静止时,圆柱体未接触容器,弹簧测力计示数为1.4N,此时容器对水平桌面的压强是( )

| A. |
7.8×10 2Pa |
B. |
8.0×10 2Pa |
C. |
9.8×10 2Pa |
D. |
1.18×10 3Pa |
如图所示,甲、乙两质地均匀的正方体放在水平地面上,它们的边长之比l甲:l乙=2:3,质量之比m甲:m乙=2:1,则它们对地面的压力之比F甲:F乙= ,对地面的压强之比p甲:p乙= 。
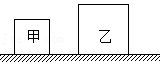
如图所示,质量分布均匀的甲,乙两个正方体叠放在水平地面上,甲放在乙的中央。若乙的边长是甲的2倍,甲对乙的压强与乙对地面的压强相等,将它们分别放入足够多的水中静止时上下表面都处于水平位置,正方体乙漂浮且有 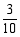 的体积浸入水中,下列判断正确的是
的体积浸入水中,下列判断正确的是 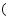
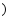

| A. |
甲、乙的质量之比 |
| B. |
甲、乙的密度之比 |
| C. |
甲、乙慢入水中的深度之比 |
| D. |
甲、乙在水中静止时所受浮力之比 |
为了说明分子之间有引力,小明在实验室用两个紧压在一起的铅柱做实验,如图所示,铅柱A和铅柱B所受的重力均为2N,两个铅柱接触面的面积为3cm2,当悬挂重物所受的重力为20N时,两个铅柱没有被拉开。于是,小明认为这个实验说明了分子之间存在引力。小华观测到该实验室的大气压为1×105Pa,于是她认为两个铅柱之所以没被拉开,是因为大气压的作用。请你利用所学知识和上述数据,判断小明做的铅柱实验能否说明分子之间存在引力。请写出计算、推理过程和结论。
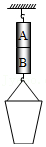
放在水平桌面上的薄壁圆柱形容器(容器质量不计)底面积为 ,将一体积为 的木块放入水中静止时,有 体积露出水面,如图甲所示;用一根质量和体积不计的细线把容器底和木块底部中心连接起来,如图乙所示。下列说法中错误的是(已知:水的密度为 ,
| A. |
木块的密度为 |
| B. |
木块漂浮时排开水的质量为 |
| C. |
浸没水中时细线对木块的拉力为 |
| D. |
甲、乙两图所示情况,容器对水平桌面的压强相等 |
某兴趣小组为检测操场上的风力等级,设计了一台简易风速仪,其工作原理如图甲所示。装有挡风板和滑片 的轻质滑块与轻质弹簧套在滑杆 上,滑杆上的摩擦力忽略不计,弹簧左端固定,右端与滑块相连。挡风板的挡风面积为0.2米 ,均匀电阻丝 长为30厘米,阻值为15欧,电源电压 恒为9伏,保护电阻 为3欧,电压表量程 伏。弹簧弹力 与弹簧长度改变量 的关系如图乙所示。无风时,滑片 在 处,有风时,滑块移动,稳定后读出电压表示数,计算并查阅如表数据可知风速及风级。
风级 |
一级 |
二级 |
三级 |
四级 |
五级 |
六级 |
风速 (米 秒) |
|
|
|
|
|
|
风压 (帕 |
|
|
|
|
|
|
(1)无风时,求通过
的电流;
(2)为保护电路安全,求出风速仪所测最大风力等级为几级;
(3)某日从天气预报得知,第二天风力等级将会达到五级,风速 预计为 ,在原有电路元件和电路基本连接方式均不变的基础上,电路将如何改进,在图丙的虚线框内将电路补充完整。小组成员还想计算出电路改进后电压表的示数,经查阅资料后得知,该挡风板所受的风压与风速的平方成正比,其关系式为 ,(其中 为常量,数值为 ,假设你为该小组成员,请你计算出风速为 时,改进后的电路中电压表的示数。
如图所示,水平桌面上甲、乙两个底面积不同的烧杯,分别盛有 、 两种不同液体,此时杯底受到液体的压强相同,将两个完全相同的小球分别放入两个烧杯中,静止后,小球在甲杯中漂浮,在乙杯中悬浮(没有液体溢出)。下列判断正确的是

A.甲烧杯中液体 的密度小于乙烧杯中液体 的密度
B.放入小球后液体对甲杯底的压力大于液体对乙杯底的压力
C.放入小球后液体对甲杯底的压强小于液体对乙杯底的压强
D.甲烧杯中小球受到的浮力等于乙烧杯中小球受到的浮力
如图所示, 是以 为支点的轻质杠杆, , , ,水平地面上的实心均匀正方体物块 重为 ,用细线与 点相连,在 点用 的力沿某方向拉杠杆,使 对地面的压力最小,且杠杆处于水平位置平衡,此时细线的拉力为 ;保持 点的拉力大小和方向以及杠杆的状态不变,要使 对地面的压强变为原来的 ,可将物块 沿竖直方向切去的质量为 。(忽略支点处的摩擦)
智能制造是第四次工业革命的核心技术,如图所示是为圆柱体涂抹防护油的智能装置。其外壳是敞口的长方体容器,距容器底面  处固定一支撑板
处固定一支撑板  ,
,  的中心有一小圆孔,圆柱体放在支撑板
的中心有一小圆孔,圆柱体放在支撑板  的正中央。长方体的左下角有注油口,防护油能够匀速注入长方体容器内部,当油的深度为
的正中央。长方体的左下角有注油口,防护油能够匀速注入长方体容器内部,当油的深度为  时,圆柱体刚好浮起离开支撑板
时,圆柱体刚好浮起离开支撑板  。随着液面升高,圆柱体竖直上浮,当油面上升到压力传感器时,停止注油,此时撑杆的
。随着液面升高,圆柱体竖直上浮,当油面上升到压力传感器时,停止注油,此时撑杆的  点对圆柱体有
点对圆柱体有  的竖直向下的压力。已知
的竖直向下的压力。已知  ,小圆孔面积
,圆柱体底面积
,小圆孔面积
,圆柱体底面积  ,圆柱体重
,圆柱体重  ,支撑板
,支撑板  的厚度不计,
的厚度不计,  取
取  。求:
。求:
(1)注油前,圆柱体对支撑板  的压强;
的压强;
(2)圆柱体刚好浮起离开支撑板  时浸入油中的体积;
时浸入油中的体积;
(3)圆柱体的高度。

如图甲,水平桌面上的容器(厚度不计)底部固定一轻质弹簧(质量和受到的浮力均不计),弹簧上端连有正方体铁块 ,铁块 上表面中心与不吸水的正方体木块 下表面中心用长为 的轻质细绳拴接(细绳质量不计,长度不可伸长), 、 处于静止状态。已知铁块 和木块 的边长均为 , , ,容器底面积 、质量 。弹簧的弹力每变化 ,弹簧的形变量改变 。 , 取 求:
(1)图甲中,容器对水平桌面的压强;
(2)向容器中缓慢注水,直到细绳恰好伸直(细绳不受力),如图乙所示。弹簧对铁块 的支持力是多大?
(3)细绳恰好伸直后继续向容器内缓慢注水,直到木块刚好全部被水浸没,水面又升高了多少?
试题篮
()