下面对命题“函数f(x)=x+ 是奇函数”的证明不是综合法的是( )
是奇函数”的证明不是综合法的是( )
A.∀x∈R且x≠0有f(﹣x)=(﹣x)+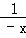 =﹣(x+ =﹣(x+ )=﹣f(x),∴f(x)是奇函数 )=﹣f(x),∴f(x)是奇函数 |
B.∀x∈R且x≠0有f(x)+f(﹣x)=x+ +(﹣x)+(﹣ +(﹣x)+(﹣ )=0,∴f(x)=﹣f(﹣x),∴f(x)是奇函数 )=0,∴f(x)=﹣f(﹣x),∴f(x)是奇函数 |
C.∀x∈R且x≠0,∵f(x)≠0,∴ = = =﹣1,∴f(﹣x)=﹣f(x),∴f(x)是奇函数 =﹣1,∴f(﹣x)=﹣f(x),∴f(x)是奇函数 |
D.取x=﹣1,f(﹣1)=﹣1+ =﹣2,又f(1)=1+ =﹣2,又f(1)=1+ =2 =2 |
推荐试卷
下面对命题“函数f(x)=x+ 是奇函数”的证明不是综合法的是( )
是奇函数”的证明不是综合法的是( )
A.∀x∈R且x≠0有f(﹣x)=(﹣x)+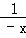 =﹣(x+ =﹣(x+ )=﹣f(x),∴f(x)是奇函数 )=﹣f(x),∴f(x)是奇函数 |
B.∀x∈R且x≠0有f(x)+f(﹣x)=x+ +(﹣x)+(﹣ +(﹣x)+(﹣ )=0,∴f(x)=﹣f(﹣x),∴f(x)是奇函数 )=0,∴f(x)=﹣f(﹣x),∴f(x)是奇函数 |
C.∀x∈R且x≠0,∵f(x)≠0,∴ = = =﹣1,∴f(﹣x)=﹣f(x),∴f(x)是奇函数 =﹣1,∴f(﹣x)=﹣f(x),∴f(x)是奇函数 |
D.取x=﹣1,f(﹣1)=﹣1+ =﹣2,又f(1)=1+ =﹣2,又f(1)=1+ =2 =2 |
试题篮
()