如图,在 中, , 为 边上一点,以 为圆心, 长为半径的 与 边相切于点 ,交 于点 .
(1)求证: ;
(2)连接 ,若 , ,求线段 的长.
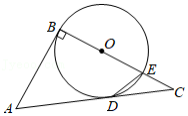
如图,在 中, , , ,以点 为圆心,3为半径的 ,与 交于点 ,过点 作 交 于点 ,点 是边 上的动点,则 的最小值为 .

如图,已知 是 的直径. 是 的弦,弦 垂直 于点 ,交 于点 .过点 作 的切线交 的延长线于点
(1)求证: ;
(2)判断 是否成立?若成立,请证明该结论;
(3)若 为 中点, , ,求 的长.
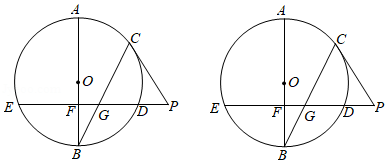
在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连接一个固定长度的“连杆”,推动“连杆”带动磨盘转动,将粮食磨碎,物理学上称这种动力传输工具为“曲柄连杆机构”.
小明受此启发设计了一个“双连杆机构”,设计图如图1,两个固定长度的“连杆” , 的连接点 在 上,当点 在 上转动时,带动点 , 分别在射线 , 上滑动, .当 与 相切时,点 恰好落在 上,如图2.
请仅就图2的情形解答下列问题.
(1)求证: ;
(2)若 的半径为5, ,求 的长.

如图,在 中, , 是 上的一点,以 为直径的 与 相切于点 ,连接 , .
(1)求证: 平分 ;
(2)若 ,求 的值.

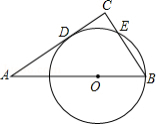
如图,在 中, , ,点 在 上, ,以 为半径的 与 相切于点 ,交 于点 ,则 的长为
| A. |
|
B. |
|
C. |
|
D. |
1 |
如图, 为 的直径,点 在 的延长线上, , 与 相切,切点分别为 , .若 , ,则 等于

| A. |
|
B. |
|
C. |
|
D. |
|
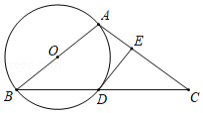
如图,在 中, ,以 为直径的 与 相交于点 ,过点 作 的切线交 于点 .
(1)求证: ;
(2)若 的半径为5, ,求 的长.
试题篮
()