如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C2015.
若P(m,2),在第2015段抛物线C2015上,则m= 6043或6044 .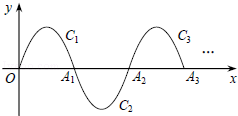
抛物线y=3x2向左平移1个单位,再向上平移2个单位,所得到的抛物线是( )
| A.y=3(x﹣1)2﹣2 |
| B.y=3(x+1)2﹣2 |
| C.y=3(x+1)2+2 |
| D.y=3(x﹣1)2+2 |
已知抛物线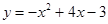 .
.
(1)求出这个抛物线的对称轴和顶点坐标;
(2)在给定的坐标系中画出这个抛物线,若抛物线与x轴交于A,B两点,与y轴交于点C,求△ABC的面积.
如图(1)是一个横断面为抛物线形状的拱桥,当水面在直线l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( )

A.y=-2 |
B.y=2 |
C.y=- |
D.y= |
二次函数y=2(x﹣1)2 +3的图象的顶点坐标是( )
| A.(1,-3) | B.(-1,3) | C.(1,3) | D.(-1,-3) |
若二次函数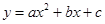 的
的 与
与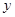 的部分对应值如下表:
的部分对应值如下表:
 |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
| y |
-27 |
-13 |
-3 |
3 |
5 |
3 |
则当 时,
时,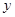 的值为( )
的值为( )
A.5 B.-3 C.-13 D.-27
在一场2015亚洲杯赛B组第二轮比赛中,中国队凭借吴曦和孙可在下半场的两个进球,提前一轮小组出线。如图,足球场上守门员在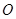 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的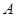 处飞出(
处飞出(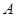 在
在 轴上),运动员孙可在距
轴上),运动员孙可在距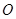 点6米的
点6米的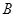 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点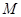 ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.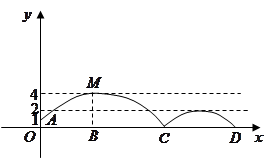
(1)求足球开始飞出到第一次落地时,该抛物线的函数表达式.
(2)足球第一次落地点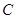 距守门员多少米?(取
距守门员多少米?(取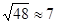 )
)
(3)孙可要抢到足球第二个落地点 ,他应从第一次落地点
,他应从第一次落地点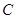 再向前跑多少米?(取
再向前跑多少米?(取 )
)
已知二次函数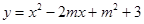 (
( 是常数).
是常数).
(1)求证:不论 为何值,该函数的图象与x轴没有公共点;
为何值,该函数的图象与x轴没有公共点;
(2)把该函数的图象沿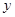 轴向下平移多少个单位长度后,得到的函数的图象与
轴向下平移多少个单位长度后,得到的函数的图象与 轴只有一个公共点?
轴只有一个公共点?
已知抛物线
(1)该抛物线的对称轴是 ,顶点坐标 ;
(2)选取适当的数据填入下表,并在直角坐标系内描点画出该抛物线的图象;
| x |
… |
|
|
|
|
|
… |
| y |
… |
|
|
|
|
|
… |
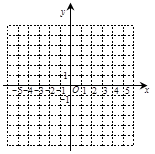
(3)若该抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足x1>x2>1,试比较y1与y2的大小.
如图,在相距2米的两棵树间拴一根绳子做一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小芳距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.

如图,抛物线y =-x2+2x+3与x轴交于点A、B,与y轴交于点C,点D是抛物线的顶点,连接BC、BD.

(1)点D的坐标是 ;
(2)在抛物线的对称轴上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标.
(3)若点P在x轴上且位于点B右侧,且点P是线段AQ的中点,连接QD,且∠BDQ=45°,求点P坐标(请利用备用图解决问题).
将二次函数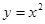 的图象向右平移1个单位,再向上平移2个单位后,所得图象的表达式是 .
的图象向右平移1个单位,再向上平移2个单位后,所得图象的表达式是 .
试题篮
()