(本小题满分12分)
已知椭圆 的离心率为
的离心率为 ,以原点
,以原点 为圆心,椭圆
为圆心,椭圆 的长半轴这半径的圆与直线
的长半轴这半径的圆与直线 相切.
相切.
(1)求椭圆 标准方程;
标准方程;
(2)已知点 为动直线
为动直线 与椭圆
与椭圆 的两个交点,问:在
的两个交点,问:在 轴上是否存在点
轴上是否存在点 ,使
,使 为定值?若存在,试求出点
为定值?若存在,试求出点 的坐标和定值,若不存在,说明理由.
的坐标和定值,若不存在,说明理由.
(本小题满分12分)
如图,已知四棱锥 中,
中, 平面
平面 ,底面
,底面 是正方形,
是正方形, 为
为 上的动点,
上的动点, 为棱
为棱 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)试确定点的位置,使得平面 平面
平面 ,并说明理由.
,并说明理由.
(本小题满分12分)
设数列 满足
满足 ,且对任意
,且对任意 ,函数
,函数 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,记数列
,记数列 的前项和为
的前项和为 ,求证:
,求证: .
.
运行如下程序框图:
若输出的的 值为12,则判断框中
值为12,则判断框中 的值可以是
的值可以是
| A.2 | B.3 | C.4 | D.5 |
下列说法中,不正确的是
A.“ ”是“ ”是“ ” 的必要不充分条件 ” 的必要不充分条件 |
B.命题“若 都是奇数,则 都是奇数,则 是奇数”的否命题是“若 是奇数”的否命题是“若 不都是奇数,则 不都是奇数,则 不是奇数” 不是奇数” |
C.命题 或 或 ,则 ,则 使 使 或 或 |
D.命题 若回归方程为 若回归方程为 ,则 ,则 与 与 正相关;命题 正相关;命题 :若 :若 ,则 ,则 ,则 ,则 为真命题 为真命题 |
已知抛物线 ,则
,则
A.它的焦点坐标为 |
B.它的焦点坐标为 |
C.它的准线方程是 |
D.它的准线方程是 |
(本小题满分10分)
已知函数 的定义域为
的定义域为 .
.
(1)求实数 的取值范围;
的取值范围;
(2)当正数 满足
满足 时,求
时,求 的最小值.
的最小值.
(本小题满分10分)
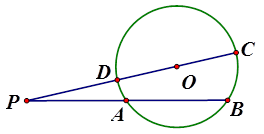
自圆 外一点
外一点 引圆
引圆 的两条割线
的两条割线 和
和 ,如图所示,其中割线
,如图所示,其中割线 过圆心
过圆心 ,
, .
.
(1)求 的大小;
的大小;
(2)分别求线段 和
和 的长度.
的长度.
(本小题满分12分)
已知函数 ,且曲线
,且曲线 在点
在点 处的切线与直线
处的切线与直线 平行.
平行.
(1)求 的值;
的值;
(2)判断函数 的单调性;
的单调性;
(3)求证:当 时,
时,
(本小题满分12分)
已知椭圆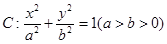 的离心率为
的离心率为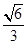 ,以原点
,以原点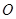 为圆心,椭圆
为圆心,椭圆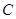 的长半轴这半径的圆与直线
的长半轴这半径的圆与直线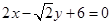 相切.
相切.
(1)求椭圆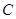 标准方程;
标准方程;
(2)已知点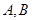 为动直线
为动直线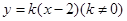 与椭圆
与椭圆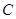 的两个交点,问:在
的两个交点,问:在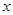 轴上是否存在点
轴上是否存在点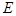 ,使
,使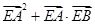 为定值?若存在,试求出点
为定值?若存在,试求出点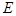 的坐标和定值,若不存在,说明理由.
的坐标和定值,若不存在,说明理由.
试题篮
()