如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
求证:(1)AM∥平面BDE;
(2)AM⊥平面BDF.
设数列{an}:1,-2,-2,3,3,3,-4,-4,-4,-4,…,(-1)k-1k,…,(-1) ,即当
,即当 (k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
(k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
设函数f(x)=x-xlnx,数列{an}满足0<a1<1,an+1=f(an).求证:
(1)函数f(x)在区间(0,1)是增函数;
(2)an<an+1<1.
已知f(n)=1+ n∈N),g(n)=2(
n∈N),g(n)=2( -1)(n∈N).
-1)(n∈N).
(1)当n=1,2,3时,分别比较f(n)与g(n)的大小(直接给出结论);
(2)由(1)猜想f(n)与g(n)的大小关系,并证明你的结论.
已知数列{an}满足a1=1,且4an+1-anan+1+2an=9(n∈N).
(1)求a2,a3,a4的值;
(2)由(1)猜想{an}的通项公式,并给出证明.
已知f(x)=ax+ (a>1).
(a>1).
(1)证明f(x)在(-1,+∞)上为增函数;
(2)用反证法证明方程f(x)=0没有负数根.
数列{an}的前n项和记为Sn,已知a1=1,an+1= Sn(n=1,2,3,…),证明:
Sn(n=1,2,3,…),证明:
(1)数列 是等比数列;
是等比数列;
(2)Sn+1=4an.
设数列 满足a1=0且
满足a1=0且 -
- = 1.
= 1.
(1) 求 的通项公式;
的通项公式;
(2) 设bn= ,记Sn=
,记Sn= ,证明:Sn<1.
,证明:Sn<1.
已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P为椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线 =1写出具有类似特性的性质,并加以证明.
=1写出具有类似特性的性质,并加以证明.
在各项为正的数列{an}中,数列的前n项和Sn满足Sn=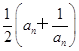 .
.
(1) 求a1,a2,a3;
(2) 由(1)猜想数列{an}的通项公式;
(3) 求Sn.
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面).当圆柱底面半径r取何值时,S取得最大值?并求出该最大值(结果精确到0.01平方米).
在△ABC中,∠BAC=90°,∠B=60°,AB=1,D为线段BC的中点,E、F为线段AC的三等分点(如图①).将△ABD沿着AD折起到△AB′D的位置,连结B′C(如图②).
图①
图②
(1)若平面AB′D⊥平面ADC,求三棱锥B′-ADC的体积;
(2)记线段B′C的中点为H,平面B′ED与平面HFD的交线为l,求证:HF∥l;
(3)求证:AD⊥B′E.
如图,在球面上有四个点P、A、B、C,如果PA、PB、PC两两互相垂直,且PA=PB=PC=a,求这个球的表面积.
如图,在直四棱柱ABCDA1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,且AB=2CD,在棱AB上是否存在一点F,使平面C1CF∥平面ADD1A1?若存在,求点F的位置;若不存在,请说明理由.
试题篮
()