高中数学试题

已知函数 $f\left(x\right)=x^3+k\mathit{ln}x(k\in R)$， $f^{\text{'}}\left(x\right)$为 $f\left(x\right)$的导函数．

（Ⅰ）当 $k=6$时，

（i）求曲线 $y=f\left(x\right)$在点 $(1,f(1\left)\right)$处的切线方程；

（ii）求函数 $g\left(x\right)=f\left(x\right)-f^{\text{'}}\left(x\right)+\frac{9}{x}$的单调区间和极值；

（Ⅱ）当 $k⩾-3$时，求证：对任意的 $x_1,\hspace{1em}{x}_2\in [1,+\infty )$，且 $x_1>x_2$，有 $\frac{f^{\text{'}}\left(x_1\right)+f^{\text{'}}\left(x_2\right)}{2}>\frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}$．

已知 $1<a\le 2$，函数 $f\left(x\right)=e^x-x-a$，其中e=2.71828…为自然对数的底数．

（Ⅰ）证明：函数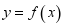在 $(0，+\infty )$上有唯一零点；

（Ⅱ）记x₀为函数在 $(0，+\infty )$上的零点，证明：

（ⅰ） $\sqrt{a-1}\le x_0\le \sqrt{2(a-1)}$；

（ⅱ） $x_{0}f(e^{x_0})\ge (e-1\left)\right(a-1)a$．

已知 $\left\{a_n\right\}$是无穷数列．给出两个性质：

①对于 $\left\{a_n\right\}$中任意两项 $a_i,a_j(i>j)$，在 $\left\{a_n\right\}$中都存在一项 $a_m$，使 $\frac{a_i^2}{a_j}=a_m$；

②对于 $\left\{a_n\right\}$中任意项 $a_n(n⩾3)$，在 $\left\{a_n\right\}$中都存在两项 $a_k,a_l(k>l)$．使得 $a_n=\frac{a_k^2}{a_l}$．

(Ⅰ)若 $a_n=n(n=1,2,\cdots )$，判断数列 $\left\{a_n\right\}$是否满足性质①，说明理由；

(Ⅱ)若 $a_n=2^{n-1}(n=1,2,\cdots )$，判断数列 $\left\{a_n\right\}$是否同时满足性质①和性质②，说明理由；

(Ⅲ)若 $\left\{a_n\right\}$是递增数列，且同时满足性质①和性质②，证明： $\left\{a_n\right\}$为等比数列.

已知函数 $f\left(x\right)=|3x+1|-2|x-1|$ ．

（1）画出 $y=f\left(x\right)$ 的图像；

（2）求不等式 $f\left(x\right)>f(x+1)$ 的解集．

已知A、B分别为椭圆E： $\frac{x^2}{a^2}+y^2=1$（a>1）的左、右顶点，G为E的上顶点， $\overrightarrow{\mathit{AG}}\cdot \overrightarrow{\mathit{GB}}=8$，P为直线x=6上的动点，PA与E的另一交点为C，PB与E的另一交点为D．

（1）求E的方程；

（2）证明：直线CD过定点.

数列 $\left\{a_n\right\}$满足 $a_{n+2}+(-1{)}^n{a}_n=3n-1$，前16项和为540，则 $a_1=$ ______________.

已知函数 $f\left(x\right)=\left|x-a^2\right|+|x-2a+1|$ .

（1）当 $a=2$ 时，求不等式 $f\left(x\right)⩾4$ 的解集；

（2）若 $f\left(x\right)⩾4$ ，求 a的取值范围.

已知曲线C₁，C₂的参数方程分别为C₁：（θ为参数），C₂： $\left\{\begin{array}{c}x=t+\frac{1}{t},\\ y=t-\frac{1}{t}\end{array}\right.$（t为参数）.

（1）将C₁，C₂的参数方程化为普通方程；

（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系.设C₁，C₂的交点为P，求圆心在极轴上，且经过极点和P的圆的极坐标方程.

设 a， b， c $\in$ R， a+ b+ c=0， abc=1．

（1）证明： ab+ bc+ ca<0；

（2）用max{ a， b， c}表示 a， b， c中的最大值，证明：max{ a， b， c}≥ $\sqrt[3]{4}$ ．

在直角坐标系 xOy中，曲线 C的参数方程为 $\left\{\begin{array}{c}x=2-t-t^2，\\ y=2-3t+t^2\end{array}\right.$ ( t为参数且 t≠1)， C与坐标轴交于 A， B两点.

（1）求| $\mathit{AB}$ |：

（2）以坐标原点为极点， x轴正半轴为极轴建立极坐标系，求直线 AB的极坐标方程.

如果对任意 $x_1,x_2\in R$ ,当 $x_1-x_2\in S$ 时, 都有 $f\left(x_1\right)-f\left(x_2\right)\in S$ ,则称 $f\left(x\right)$ 是 $S$ 关联的.

(1)判断和证明 $f\left(x\right)=2x-1$ 是 $Z^{+}$ 关联的吗?是 $\left[0,1\right]$ 关联的吗?

(2) $f\left(x\right)$ 是 $\left\{3\right\}$ 关联的,当 $x\in [0,3)$ 时， $f\left(x\right)=x^2-2x$ ,解不等式 $2⩽f\left(x\right)⩽3$ .

(3)" $f\left(x\right)$ 是 $\left\{1\right\}$ 关联的,且是 $[0,+\infty )$ 关联的"当且仅当" $f\left(x\right)$ 是 $\left[1,2\right]$ 关联的"

定义 $R_p$ 数列 $\left\{a_n\right\}:$ 对 $p\in R$, 满足:

① $a_1+p⩾0,a_2+p=0$;

② $\forall n\in N^{*},a_{4n-1}<a_{4n}$;

③ $\forall m,n\in N^{*},a_{m+n}\in \left\{a_m+a_n+p,a_m+a_n+p+1\right\}$.

(1) 对前 4 项 $2,-2,0,1$ 的数列, 可以是 $R_2$ 数列吗? 说明理由.

(2) 若 $\left\{a_n\right\}$ 是 $R_0$ 数列, 求 $a_5$ 的值.

(3) 是否存在 $p\in R$, 使得存在 $R_p$ 数列 $\left\{a_n\right\}$, 对任意 $n\in N^{*}$, 满足 $S_n⩾S_{10}$ ? 若存在, 求出所有这样的 $p$; 若不存在, 请说明理由.

设a，b为实数，且 $a>1$，函数 $f\left(x\right)=a^x-\mathit{bx}+e^2(x\in R)$

（1）求函数 $f\left(x\right)$的单调区间；

（2）若对任意 $b>2e^2$，函数 $f\left(x\right)$有两个不同的零点，求a的取值范围；

（3）当 $a=e$时，证明：对任意 $b>e^4$，函数 $f\left(x\right)$有两个不同的零点 $x_1,x_2$，满足 $x_2>\frac{b\mathit{ln}b}{2e^2}{x}_1+\frac{e^2}{b}$.

(注： $e=2.71828\cdot \cdot \cdot$是自然对数的底数)

已知函数 $f\left(x\right)=(x-1)e^x-a{x}^2+b$．

（1）讨论 $f\left(x\right)$的单调性；

（2）从下面两个条件中选一个，证明： $f\left(x\right)$有一个零点

① $\frac{1}{2}<a\le \frac{e^2}{2},b>2a$；

② $0<a<\frac{1}{2},b\le 2a$．

已知函数 $f\left(x\right)=x\left(1-\mathit{ln}x\right)$.

（1）讨论 $f\left(x\right)$的单调性；

（2）设 $a$， $b$为两个不相等的正数，且 $b\mathit{ln}a-a\mathit{ln}b=a-b$，证明： $2<\frac{1}{a}+\frac{1}{b}<e$.