甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若未命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为 ,乙每次投篮的命中率均为 .由抽签确定第 次投篮的人选,第 次投篮的人是甲、乙的概率各为 .
(1)求第 次投篮的人是乙的概率;
(2)求第 次投篮的人是甲的概率;
(3)已知:若随机变量 服从两点分布,且 , 则 .记前 次(即从第 次到第 次投篮)中甲投篮的次数为 ,求 .
设等差数列 的公差为 ,且 .令 ,记 , 分别为数列 , 的前 项和.
(1)若 , ,求 的通项公式;
(2)若 为等差数列,且 ,求 .
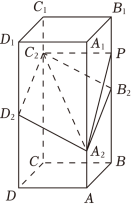
如图,在正四棱柱 中, , .点 , , , 分别在棱 , , , 上, , , .
(1)证明: ;
(2)点 在棱 上,当二面角 为 时,求 .
[选修4-5:不等式选讲]
已知 .
(1)求不等式 的解集;
(2)在直角坐标系 中,求不等式组 所确定的平面区域的面积.
[选修4-4:坐标系与参数方程]
在直角坐标系 中,以坐标原点 为极点, 轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为 ,曲线 ( 为参数, ).
(1)写出 的直角坐标方程;
(2)若直线 既与 没有公共点,也与 没有公共点、求 的取值范围.
已知椭圆 的离心率为 ,点 在 上.
(1)求 的方程;
(2)过点 的直线交 于点 , 两点,直线 , 与 轴的交点分别为 , ,证明:线段 的中点为定点.
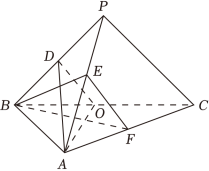
如图,在三棱锥 中, , , , , , , , 的中点分别为 , , ,点 在 上, .
(1)证明: 平面 ;
(2)证明:平面 平面 ;
(3)求二面角 的正弦值.
某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应,进行 次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后的橡胶产品的伸缩率,甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为 , .试验结果如下:
|
试验序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
伸缩率 |
545 |
533 |
551 |
522 |
575 |
544 |
541 |
568 |
596 |
548 |
|
伸缩率 |
536 |
527 |
543 |
530 |
560 |
533 |
522 |
550 |
576 |
536 |
记 ,记 的样本平均数为 ,样本方差为 .
(1)求 , ;
(2)判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高.(如果 ,则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高,否则不认为有显著提高)
[选修4-5:不等式选讲]
已知 .
(1)求不等式 的解集;
(2)在直角坐标系 中,求不等式组 所确定的平面区域的面积.
[选修4-4:坐标系与参数方程]
在直角坐标系 中,以坐标原点 为极点, 轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为 ,曲线 ( 为参数, ).
(1)写出 的直角坐标方程;
(2)若直线 既与 没有公共点,也与 没有公共点、求 的取值范围.
已知椭圆 的离心率为 ,点 在 上.
(1)求 的方程;
(2)过点 的直线交 于点 , 两点,直线 , 与 轴的交点分别为 , ,证明:线段 的中点为定点.
试题篮
()