高中数学解答题

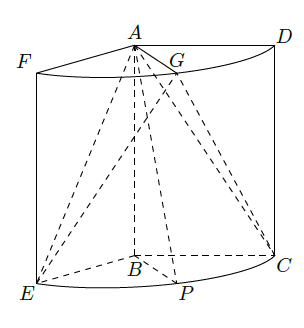
如图，几何体是圆柱的一部分，它是由矩形ABCD（及其内部）以AB边所在直线为旋转轴旋转120°得到的，G是 $\stackrel{̂}{\mathit{DF}}$ 的中点．

（Ⅰ）设P是 $\stackrel{̂}{\mathit{CE}}$ 上的一点，且 $\mathit{AP}\perp \mathit{BE}$ ，求 $\angle \mathit{CBP}$ 的大小；

（Ⅱ）当 $\mathit{AB}=3$ ， $\mathit{AD}=2$ 时，求二面角 $E﹣\mathit{AG}﹣C$ 的大小．

设函数 $f（x）=\mathit{sin}\left(\omega x﹣\frac{\pi }{6}\right)+\mathit{sin}\left(\omega x﹣\frac{\pi }{2}\right)$ ，其中 $0＜\omega ＜3$ ，已知 $f（\frac{\pi }{6}）=0$ ．

（Ⅰ）求 $\omega$ ；

（Ⅱ）将函数 $y=f\left(x\right)$ 的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移 $\frac{\pi }{4}$ 个单位，得到函数 $y=g\left(x\right)$ 的图象，求 $g\left(x\right)$ 在 $\left[﹣\frac{\pi }{4}，\frac{3\pi }{4}\right]$ 上的最小值．

[选修4―4：坐标系与参数方程]

在直角坐标系 xOy中，直线 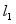$l_1$ 的参数方程为 $\left\{\begin{array}{c}x=2+t,\\ y=\mathit{kt},\end{array}\right.$ （ t为参数），直线 $l_2$ 的参数方程为 $\left\{\begin{array}{c}x=-2+m,\\ y=\frac{m}{k},\end{array}\right.（m\mathit{为参数）}$ .设 l ₁与 l ₂的交点为 P，当 k变化时， P的轨迹为曲线 C ．

（1）写出 C的普通方程；

（2）以坐标原点为极点， x轴正半轴为极轴建立极坐标系，设 $l3：\rho (\mathit{cos}\theta +\mathit{sin\theta })-\sqrt{2}=0$ ， M为 l ₃与 C的交点，求 M的极径.

在直角坐标系 $\mathit{xOy}$ 中，曲线 $y=x^2+\mathit{mx}-2$ 与x轴交于A，B两点，点C的坐标为 $(0,1)$ .当m变化时，解答下列问题：

（1）能否出现 $\mathit{AC}\perp \mathit{BC}$ 的情况？说明理由；

（2）证明过 A， B， C三点的圆在 y轴上截得的弦长为定值.

如图，四面体ABCD中，△ABC是正三角形， $\mathit{AD}=\mathit{CD}$ ．

（1）证明： $\mathit{AC}\perp \mathit{BD}$ ；

（2）已知△ACD是直角三角形， $\mathit{AB}=\mathit{BD}$．若E为棱BD上与D不重合的点，且 $\mathit{AE}\perp \mathit{EC}$ ，求四面体ABCE与四面体ACDE的体积比．

某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[20，25），需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：

最高气温	$[10，15）$	$[15，20）$	$[20，25）$	$[25，30）$	$[30，35）$	$[35，40）$
天数	2	16	36	25	7	4

以最高气温位于各区间的频率代替最高气温位于该区间的概率。

（1）求六月份这种酸奶一天的需求量不超过300瓶的概率；

（2）设六月份一天销售这种酸奶的利润为 $Y$ （单位：元），当六月份这种酸奶一天的进货量为450瓶时，写出 $Y$ 的所有可能值，并估计 $Y$ 大于零的概率．

设数列 $\left\{a_n\right\}$ 满足 $a_1+3a_2+\dots +(2n-1)a_n=2n$ .

（1）求 $\left\{a_n\right\}$ 的通项公式；

（2）求数列 $\left\{\frac{a_n}{2_n+1}\right\}$ 的前 $n$ 项和.

设 ${(1+x)}^n=a_0+a_{1}x+a_2{x}^2+\cdots +a_n{x}^n,n⩾4,n\in N^{*}$ .已知 $a_3^2=2a_2{a}_4$ .   

（1）求 n的值；    

（2）设 ${(1+\sqrt{3})}^n=a+b\sqrt{3}$ ，其中 $a,b\in N^{*}$ ，求 $a^2-3b^2$ 的值.    

设 $x\in R$ ，解不等式 $\text{|}x\text{|+|2}x-\text{1|>2}$ .   

在极坐标系中，已知两点 $A(3,\frac{\pi }{4}),B(\sqrt{2},\frac{\pi }{2})$ ，直线l的方程为 $\rho \sin (\theta +\frac{\pi }{4})=3$ .

（1）求 A， B两点间的距离；    

（2）求点 B到直线 l的距离.    

已知矩阵 $A=\left[\begin{array}{cc}3& 1\\ 2& 2\end{array}\right]$

（1）求 A ²；    

（2）求矩阵 A的特征值.   

定义首项为1且公比为正数的等比数列为"M－数列".   

（1）已知等比数列{ a _n} $(n\in N^{*})$ 满足： $a_2{a}_4=a_5,a_3-4a_2+4a_4=0$ ，求证:数列{ a _n}为"M－数列"；    

（2）已知数列{ b _n}满足: $b_1=1,\frac{1}{S_n}=\frac{2}{b_n}-\frac{2}{b_{n+1}}$ ，其中 S _n为数列{ b _n}的前 n项和．

①求数列{ b _n}的通项公式；

②设 m为正整数，若存在"M－数列"{ c _n} $(n\in N^{*})$ ，对任意正整数 k ，当 k≤ m时，都有 $c_k⩽b_k⩽c_{k+1}$ 成立，求 m的最大值．

设函数 $f\left(x\right)=(x-a)(x-b)(x-c),a,b,c\in \text{R}$ 、 $f\text{'}\left(x\right)$ 为f（x）的导函数．   

（1）若 a= b= c ， f（4）=8，求 a的值；    

（2）若 a≠ b ， b= c ， 且 f（ x）和 $f\text{'}\left(x\right)$ 的零点均在集合 $\text{{}-3,1,3\text{}}$ 中，求 f（ x）的极小值；    

（3）若 $a=0,0<b⩽1,c=1$ ，且 f（ x）的极大值为 M，求证: M≤ $\frac{4}{27}$ ．

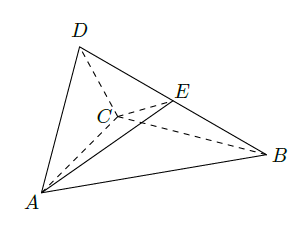
如图，一个湖的边界是圆心为O的圆，湖的一侧有一条直线型公路l ，湖上有桥AB（AB是圆O的直径）．规划在公路l上选两个点P、Q ，并修建两段直线型道路PB、QA ．规划要求:线段PB、QA上的所有点到点O的距离均不小于圆O的半径．已知点A、B到直线l的距离分别为AC和BD（C、D为垂足），测得AB=10，AC=6，BD=12（单位:百米）．

（1）若道路PB与桥AB垂直，求道路PB的长；   

（2）在规划要求下，P和Q中能否有一个点选在D处？并说明理由；   

（3）对规划要求下，若道路PB和QA的长度均为d（单位：百米）.求当d最小时，P、Q两点间的距离．

如图，在平面直角坐标系xOy中，椭圆C: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的焦点为F ₁（-1、0），F ₂（1，0）．过F ₂作x轴的垂线l ，在x轴的上方，l与圆F ₂: ${(x-1)}^2+y^2=4a^2$ 交于点A ，与椭圆C交于点D.连结AF ₁并延长交圆F ₂于点B ，连结BF ₂交椭圆C于点E ，连结DF ₁．已知DF ₁= $\frac{5}{2}$ ．

（1）求椭圆 C的标准方程；    

（2）求点 E的坐标．