记 为等差数列 的前 项和,已知 , .
(1)求 的通项公式;
(2)求数列 的前 项和 .
某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应,进行 次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后的橡胶产品的伸缩率,甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为 , .试验结果如下:
|
试验序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
伸缩率 |
545 |
533 |
551 |
522 |
575 |
544 |
541 |
568 |
596 |
548 |
|
伸缩率 |
536 |
527 |
543 |
530 |
560 |
533 |
522 |
550 |
576 |
536 |
记 ,记 的样本平均数为 ,样本方差为 .
(1)求 , ;
(2)判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高.(如果 ,则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高,否则不认为有显著提高)
已知抛物线方程 , 为焦点, 为抛物线准线上一点, 为线段 与抛物线的交点,定义: .
(1)当 时,求 ;
(2)证明:存在常数 ,使得 ;
(3) , , 为抛物线准线上三点,且 ,判断 与 的关系.
改革开放40年,我国卫生事业取得巨大成就,卫生总费用增长了数十倍.卫生总费用包括个人现在支出、社会支出、政府支出,如表为2012年 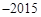 年我国卫生货用中个人现金支出、社会支出和政府支出的费用(单位:亿元)和在卫生总费用中的占比.
年我国卫生货用中个人现金支出、社会支出和政府支出的费用(单位:亿元)和在卫生总费用中的占比.
| 年份 |
卫生总费用(亿元) |
个人现金卫生支出 |
社会卫生支出 |
政府卫生支出 |
|||
| 绝对数(亿元) |
占卫生总费用比重 |
绝对数(亿元) |
占卫生总费用比重 |
绝对数(亿元) |
占卫生总费用比重 |
||
| 2012 |
28119.00 |
9656.32 |
34.34 |
10030.70 |
35.67 |
8431.98 |
29.99 |
| 2013 |
31668.95 |
10729.34 |
33.88 |
11393.79 |
35.98 |
9545.81 |
30.14 |
| 2014 |
35312.40 |
11295.41 |
31.99 |
13437.75 |
38.05 |
10579.23 |
29.96 |
| 2015 |
40974.64 |
11992.65 |
29.27 |
16506.71 |
40.29 |
12475.28 |
30.45 |
(数据来源于国家统计年鉴)
(1)指出2012年到2015年之间我国卫生总费用中个人现金支出占比和社会支出占比的变化趋势:
(2)设 表示1978年,第 年卫生总费用与年份 之间拟合函数 研究函数 的单调性,并预测我国卫生总费用首次超过12万亿的年份.
已知数列 , ,前 项和为 .
(1)若 为等差数列,且 ,求 ;
(2)若 为等比数列,且 ,求公比 的取值范围.
如图,在正三棱锥 中, , .
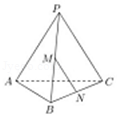
(1)若 的中点为 , 的中点为 ,求 与 的夹角;
(2)求 的体积.
已知椭圆 的右焦点为 ,且经过点 .
(Ⅰ)求椭圆 C的方程;
(Ⅱ)设 O为原点,直线 与椭圆 C交于两个不同点 P, Q,直线 与 x轴交于点 M,直线 与 x轴交于点 N,若 ,求证:直线 l经过定点.
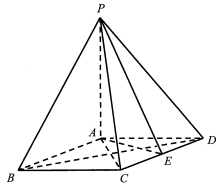
如图,在四棱锥 中, ,底部 ABCD为菱形, E为 CD的中点.
(Ⅰ)求证: ;
(Ⅱ)若 ,求证: ;
(Ⅲ)棱 PB上是否存在点 F,使得 ?说明理由.
改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
| 支付金额 支付方式 |
不大于 元 |
大于 元 |
| 仅使用A |
27人 |
3人 |
| 仅使用B |
24人 |
1人 |
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于 元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于 元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于 元的人数有变化?说明理由.
设 是等差数列, ,且 , , 成等比数列.
(Ⅰ)求 的通项公式;
(Ⅱ)记 的前 n项和为 ,求 的最小值.
已知函数 , ,其中 是自然对数的底数.
(Ⅰ)求曲线 在点 处的切线方程;
(Ⅱ)令 ,讨论 的单调性并判断有无极值,有极值时求出极值.
已知 是各项均为正数的等比数列,且 , .
(Ⅰ)求数列 的通项公式;
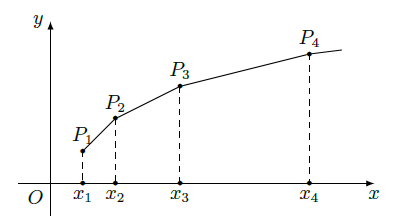
(Ⅱ)如图,在平面直角坐标系 中,依次连接点 , 得到折线 , 求由该折线与直线 , , 所围成的区域的面积 .
在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A 1 , A 2 , A 3 , A 4 , A 5 , A 6和4名女志愿者B 1 , B 2 , B 3 , B 4 , 从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(Ⅰ)求接受甲种心理暗示的志愿者中包含A 1但不包含B 1的概率.
(Ⅱ)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
试题篮
()