下列命题:①△ABC的三边分别为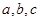 则该三角形是等边三角形的充要条件为
则该三角形是等边三角形的充要条件为 ;②数列
;②数列 的前n项和为
的前n项和为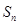 ,则
,则 是数列
是数列 为等差数列的必要不充分条件;③在△ABC中,A=B是sin A=sin B的充分必要条件;④已知
为等差数列的必要不充分条件;③在△ABC中,A=B是sin A=sin B的充分必要条件;④已知 都是不等于零的实数,关于
都是不等于零的实数,关于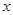 的不等式
的不等式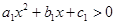 和
和 的解集分别为P,Q,则
的解集分别为P,Q,则 是
是 的充分必要条件,其中正确的命题是( )
的充分必要条件,其中正确的命题是( )
| A.①④ | B.①②③ | C.②③④ | D.①③ |
设a,b为正实数,则“a>b>1”是“log2a>log2b>0”的( )
| A.充要条件 |
| B.充分不必要条件 |
| C.必要不充分条件 |
| D.既不充分也不必要条件 |
下列说法中,不正确的是( )
A.已知 ,命题“若 ,命题“若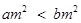 ,则 ,则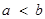 ”为真命题; ”为真命题; |
B.命题“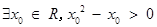 ”的否定是:“ ”的否定是:“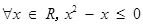 ”; ”; |
C.命题“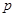 或 或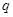 ”为真命题,则命题 ”为真命题,则命题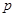 和命题 和命题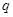 均为真命题; 均为真命题; |
D.“ ”是“ ”是“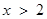 ”的充分不必要条件. ”的充分不必要条件. |
数列{xn}满足x1=0,xn+1=-xn2+xn+c(n∈N*).
(1)证明:{xn}是递减数列的充分必要条件是c<0;
(2)求c的取值范围,使{xn}是递增数列.
给出下列四个命题, 其中正确的命题有
 个.
个.
(1)函数 上的单调递增区间是
上的单调递增区间是 ;
;
(2) 均为非零实数,集合
均为非零实数,集合 ,则“
,则“ ”是“
”是“ ”的必要不充分条件
”的必要不充分条件
(3)若 为真命题,则
为真命题,则 也为真命题
也为真命题
(4) 命题 的否定
的否定
A. |
B. |
C. |
D. |
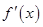 是定义在
是定义在 上的函数
上的函数 的导函数,
的导函数, ,设命题
,设命题 :
: ;命题
;命题 :
: 是函数
是函数 的极值点,则
的极值点,则 是
是 成立的( )
成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知P={x|x2﹣8x﹣20≤0},S={x|1﹣m≤x≤1+m}
(1)是否存在实数m,使x∈P是x∈S的充要条件,若存在,求出m的取值范围;
(2)是否存在实数m,使x∈P是x∈S的必要条件,若存在,求出m的取值范围.
给出下列四个命题:
①命题“ ”的否定是“
”的否定是“ ”;
”;
②“ ”是“直线
”是“直线 与直线
与直线 相互垂直”的必要不充分条件;
相互垂直”的必要不充分条件;
③设圆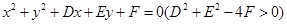 与坐标轴有4个交点,分别为
与坐标轴有4个交点,分别为 ,则
,则 ;
;
④关于 的不等式
的不等式 的解集为
的解集为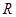 ,则
,则 .
.
其中所有真命题的序号是 .
已知命题 “存在
“存在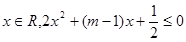 ”,命题
”,命题 :“曲线
:“曲线 表示焦点在
表示焦点在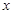 轴上的椭圆”,命题
轴上的椭圆”,命题 “曲线
“曲线 表示双曲线”
表示双曲线”
(1)若“ 且
且 ”是真命题,求
”是真命题,求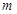 的取值范围;
的取值范围;
(2)若 是
是 的必要不充分条件,求
的必要不充分条件,求 的取值范围。
的取值范围。
试题篮
()