给出下列四个命题:
①如果命题“¬p”与命题“p∨q”都是真命题,那么命题q一定是真命题;
②命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”;
③若命题p:∃x≥0,x2﹣x+1<0,则¬p:∀x<0,x2﹣x+1≥0;
④设{an}是首项大于零的等比数列,则“a1<a2”是“数列{an}是递增数列”的充分而不必要条件.
其中为真命题的个数是( )
| A.4个 | B.3个 | C.2个 | D.1个 |
下列命题正确的个数是( )
①命题“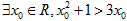 ”的否定是“
”的否定是“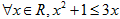 ”;
”;
②“函数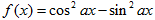 的最小正周期为
的最小正周期为 ”是“
”是“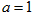 ”的必要不充分条件;
”的必要不充分条件;
③ 在
在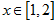 上恒成立
上恒成立
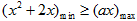 ,
, ;
;
④“平面向量 与
与 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“ ”.
”.
| A.1 | B.2 | C.3 | D.4 |
下列说法错误的是( )
A. 是 是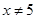 或 或 的充分不必要条件 的充分不必要条件 |
B.若命题 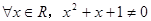 ,则 ,则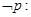  |
C.线性相关系数 的绝对值越接近 的绝对值越接近 ,表示两变量的相关性越强. ,表示两变量的相关性越强. |
| D.用频率分布直方图估计平均数,可以用每个小矩形的高乘以底边中点横坐标之后加和 |
下列结论正确的个数是( )
①若 ,则
,则 ;
;
②命题“ ,
,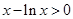 ”的否定是“
”的否定是“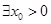 ,
, ”;
”;
③“命题 为真”是“命题
为真”是“命题 为真”的充分不必要条件.
为真”的充分不必要条件.
A.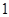 个 个 |
B. 个 个 |
C.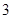 个 个 |
D. 个 个 |
有四个命题
①p:f(x)=lnx﹣2+λ在区间(1,2)上有一个零点,q:e0.2>e0.3,p∧q为真命题
②当x>1时,f(x)=x2,g(x)=x ,h(x)=x﹣2的大小关系是h(x)<g(x)<f(x)
,h(x)=x﹣2的大小关系是h(x)<g(x)<f(x)
③若f′(x0)=0,则f(x)在x=x0处取得极值
④若不等式2﹣3x﹣2x2>0的解集为P,函数y= +
+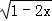 的定义域为Q,则“x∈P”是“x∈Q”的充分不必要条件,其中正确命题的个数是( )
的定义域为Q,则“x∈P”是“x∈Q”的充分不必要条件,其中正确命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
下列命题中正确命题的个数是( )
(1)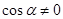 是
是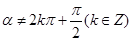 的充分必要条件
的充分必要条件
(2) 则
则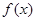 最小正周期是
最小正周期是
(3)若将一组样本数据中的每个数据都加上同一个常数后, 则样本的方差不变
(4)设随机变量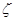 服从正态分布
服从正态分布 ,若
,若 ,则
,则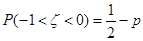
| A.4 | B.3 | C.2 | D.1 |
给出如下三个命题:
①设a,b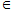 R,且
R,且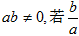 >1,则
>1,则 <1;
<1;
②四个非零实数a、b、c、d依次成等比数列的充要条件是ad=bc;
③在ΔABC中,A>B的充要条件是sinA>sinB.
其中正确命题的序号是( )
(A)①② (B)②③ (C)①③ (D)①②③
试题篮
()