如图所示,在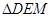 中,
中,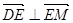 ,
,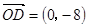 ,N在y轴上,且
,N在y轴上,且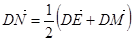 ,点E在x轴上移动.
,点E在x轴上移动.
(Ⅰ)求点M的轨迹方程;
(Ⅱ)过点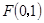 作互相垂直的两条直线
作互相垂直的两条直线 ,
, 与点M的轨迹交于点A、B,
与点M的轨迹交于点A、B,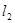 与点M的轨迹交于点C、D,求
与点M的轨迹交于点C、D,求 的最小值.
的最小值.
物体W的质量为50千克,用绳子将物体W悬挂在两面墙之间,已知两面墙之间的距离AB=10米(AB为水平线),AC=6米,BC=8米,求AC,BC上所受的力的大小。
(Ⅰ)如图1 ,
,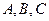 是平面内的三个点,且
是平面内的三个点,且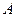 与
与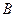 不重合,
不重合,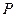 是平面内任意一点,若点
是平面内任意一点,若点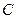 在直线
在直线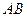 上,试证明:存在实数
上,试证明:存在实数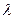 ,使得:
,使得: .
.
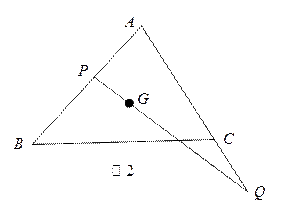
(Ⅱ)如图2,设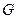 为
为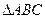 的重心,
的重心,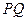 过
过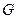 点且与
点且与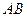 、
、 (或其延长线)分别交于
(或其延长线)分别交于 点,若
点,若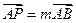 ,
,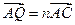 ,试探究:
,试探究: 的值是否为定值,若为定值,求出这个
的值是否为定值,若为定值,求出这个
定值;若不是定值,请说明理由.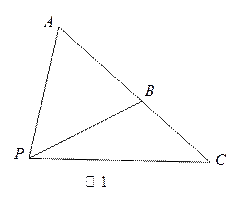
在平面内有两个向量 ,今有动点P从
,今有动点P从 开始沿着与向量
开始沿着与向量 相同方向做匀速直线运动,速度为︱
相同方向做匀速直线运动,速度为︱ ︱;另一动点Q从点
︱;另一动点Q从点 (-2,-
(-2,- 1)出发,沿着与向量
1)出发,沿着与向量 相同的方向做匀速直线运动,速度为︱
相同的方向做匀速直线运动,速度为︱ ︱,设点P、Q在时刻t=0秒时分别在
︱,设点P、Q在时刻t=0秒时分别在 、
、 处,求PQ⊥
处,求PQ⊥
 时,用了多长时间
时,用了多长时间
试题篮
()