甲,乙,丙,丁四位同学各自对A,B两变量的线性相关试验,并用回归分析方法分别求得相关系数r如表:
| |
甲 |
乙 |
丙 |
丁 |
| r |
0.82 |
0.78 |
0.69 |
0.85 |
则这四位同学的试验结果能体现出A,B两变量有更强的线性相关性的是( ).
A.甲 B.乙 C.丙 D.丁
在两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关系数r如下,其中拟合效果最好的模型是( )
| A.模型1的相关系数r为0.98 |
| B.模型2的相关系数r为0.80 |
| C.模型3的相关系数r为0.50 |
| D.模型4的相关系数r为0.25 |
已知 、
、 取值如下表:
取值如下表:
 |
0 |
1 |
4 |
5 |
6 |
 |
1.3 |
 |
 |
5.6 |
7.4 |
画散点图分析可知: 与
与 线性相关,且求得回归方程为
线性相关,且求得回归方程为 ,则
,则 的值(精确到0.1)为( )
的值(精确到0.1)为( )
A.1.5 B.1.6 C.1.7 D.1.8
观察下列关于两个变量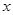 和
和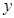 的三个散点图,它们从左到右的对应关系依次为( ).
的三个散点图,它们从左到右的对应关系依次为( ).
| A.正相关、负相关、不相关 |
| B.负相关、不相关、正相关 |
| C.负相关、正相关、不相关 |
| D.正相关、不相关、负相关 |
已知变量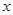 与
与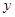 正相关,且由观测数据算得样本平均数
正相关,且由观测数据算得样本平均数 ,
, ,则由该观测数据算得的线性回归方程可能是( )
,则由该观测数据算得的线性回归方程可能是( )
A.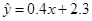 |
B. |
C.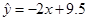 |
D. |
已知变量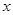 与
与 正相关,且由观测数据算得样本平均数
正相关,且由观测数据算得样本平均数 ,
,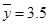 ,则由该观测数据算得的线性回归方程可能是( )
,则由该观测数据算得的线性回归方程可能是( )
A.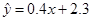 |
B.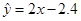 |
C.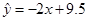 |
D.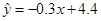 |
以下有关线性回归分析的说法不正确的是
A.通过最小二乘法得到的线性回归直线经过样本的中心 |
B.用最小二乘法求回归直线方程,是寻求使 最小的a,b的值 最小的a,b的值 |
| C.相关系数r越小,表明两个变量相关性越弱 |
D.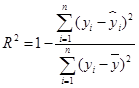 越接近1,表明回归的效果越好 越接近1,表明回归的效果越好 |
某产品的广告费用x与销售额y的统计数据如表:
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
54 |
根据上表可得回归方程 ,其中
,其中 =9.4,据此模型预报广告费用为6万元时,销售额为 ( ).
=9.4,据此模型预报广告费用为6万元时,销售额为 ( ).
A.63.6万元 B.65.5万元 C.67.7万元 D.72.0万元
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是 ( )
A.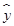 =-10x+200 =-10x+200 |
B.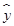 =10x+200 =10x+200 |
C.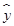 =-10x-200 =-10x-200 |
D.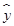 =10x-200 =10x-200 |
试题篮
()