设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为 =0.85x-85.71,则下列结论中不正确的是( ).
=0.85x-85.71,则下列结论中不正确的是( ).
| A.y与x具有正的线性相关关系 |
B.回归直线过样本点的中心( , , ) ) |
| C.若该大学某女生身高增加1 cm,则其体重约增加0.85 kg |
| D.若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg |
两个变量x,y与其线性相关系数r有下列说法
(1)若r>0,则x增大时,y也相应增大;
(2)若|r|越趋近于1,则x, y线性相关程度越强;
(3)若r=1或r=-1,则x与y的关系完全对应(有函数关系),在散点图上各个散点均在一条直线上,其中正确的有( )
| A.①② | B.②③ | C.①③ | D.①②③ |
对变量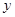 与
与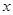 ,分别选择了4个不同的回归方程甲、乙、丙、丁,它们的相关系数
,分别选择了4个不同的回归方程甲、乙、丙、丁,它们的相关系数 分别为:
分别为:  ,
,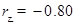 ,
, 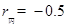 ,
,  . 其中拟合效果最好的是方程( ).
. 其中拟合效果最好的是方程( ).
| A.甲 | B.乙 | C.丙 | D.丁 |
对于线性相关系数 ,叙述正确的是
,叙述正确的是
A.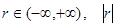 越大,相关程度越大,反之相关程度越小 越大,相关程度越大,反之相关程度越小 |
B.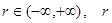 越大,相关程度越大,反之相关程度越小 越大,相关程度越大,反之相关程度越小 |
C.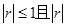 越接近1,相关程度越大 越接近1,相关程度越大 |
| D.以上说法都不对 |
对两个变量 和
和 进行回归分析,得到一组样本数据:
进行回归分析,得到一组样本数据: ,则下列说法中不正确的是( )
,则下列说法中不正确的是( )
A.由样本数据得到的回归方程 必过样本中心 必过样本中心 |
| B.残差平方和越小的模型,拟合的效果越好 |
C.用相关指数 来刻画回归效果, 来刻画回归效果, 越小,说明模型的似合效果越好 越小,说明模型的似合效果越好 |
D.若变量y和x之间的相关系数为 ,则变量y和x之间具有线性相关关系 ,则变量y和x之间具有线性相关关系 |
以下有关线性回归分析的说法不正确的是( )
A.通过最小二乘法得到的线性回归直线经过样本的中心 |
B.用最小二乘法求回归直线方程,是寻求使 最小的a,b的值 最小的a,b的值 |
| C.在回归分析中,变量间的关系若是非确定性关系,但因变量也能由自变量唯一确定 |
| D.如果回归系数是负的,y的值随x的增大而减小 |
利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅下表来确定断言“X和Y有关系”的可信度。如果k>5.024,那么就有把握认为“X和Y有关系”的百分比为( )
| P(k2>k) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.84 |
5.024 |
6.635 |
7.879 |
10.83 |
A.25% B.75% C.2.5% D.97.5%
如果数据 、
、 、……
、…… 的平均值为
的平均值为 ,方差为
,方差为 ,则
,则 ,
, ,……
,……  的平均值和方差分别为( )
的平均值和方差分别为( )
A. 和 和 |
B.3 +5和9 +5和9 |
C.3 +5和 +5和 |
D.3 +5 和9 +5 和9 +30 +30 +25 +25 |
两个变量 与
与 的回归模型中,分别选择了4个不同模型,它们的相关指数
的回归模型中,分别选择了4个不同模型,它们的相关指数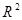 如下 ,其中拟合效果最好的模型是( )
如下 ,其中拟合效果最好的模型是( )
A.模型1的相关指数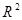 为0.98 为0.98 |
B.模型2的相关指数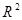 为0.80 为0.80 |
C.模型3的相关指数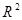 为0.50 为0.50 |
D.模型4的相关指数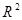 为0.25 为0.25 |
下面是2×2 列联表
| x y |
y 1 |
y 2 |
合计 |
| x1 |
a |
21 |
73 |
| x2 |
2 |
25 |
27 |
| 合计 |
b |
46 |
100 |
则表中 a 、b 处的值分别为( )
A.94 、96 B.52 、50 C.52 、54 D.54 、52
为了解儿子身高与其父亲身高的关系,随机抽取5对父子身高数据如下
| 父亲身高x(cm) |
174 |
176 |
176 |
176 |
178 |
| 儿子身高y(cm) |
175 |
175 |
176 |
177 |
177 |
则y对x的线性回归方程为 ( )
A. B.
B.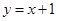 C.
C. D.
D.
试题篮
()