对变量 有观测数据(
有观测数据( ,
, )(
)( ),得散点图1;对变量
),得散点图1;对变量 有观测数据(
有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断
| A.变量x 与y 正相关,u 与v 正相关 | B.变量x 与y 正相关,u 与v 负相关 |
| C.变量x 与y 负相关,u 与v 正相关 | D.变量x 与y 负相关,u 与v 负相关 |
在两个变量y与x的回归模型中,分别选择了4个不同模型,它们的 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )
A.模型1的 为0.975 为0.975 |
B.模型2的 为0.79 为0.79 |
C.模型3的 为0.55 为0.55 |
D.模型4的 为0.25 为0.25 |
在独立性检验中,统计量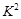 有两个临界值:3.841和6.635;当
有两个临界值:3.841和6.635;当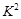 >3.841时,有95%的把握说明两个事件有关,当
>3.841时,有95%的把握说明两个事件有关,当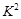 >6.635时,有99%的把握说明两个事件有关,当
>6.635时,有99%的把握说明两个事件有关,当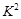
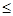 3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的
3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的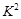 =20.87,根据这一数据分析,认为打鼾与患心脏病之间
=20.87,根据这一数据分析,认为打鼾与患心脏病之间
| A.有95%的把握认为两者有关 | B.约有95%的打鼾者患心脏病 |
| C.有99%的把握认为两者有关 | D.约有99%的打鼾者患心脏病 |
下列说法错误的是( )
| A.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系; |
B.线性回归方程对应的直线 = = x+ x+ 至少经过其样本数据(x1,y1),(x2,y2),,(xn,yn)中的一个点; 至少经过其样本数据(x1,y1),(x2,y2),,(xn,yn)中的一个点; |
| C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高; |
D.在回归分析中, 为0.98的模型比 为0.98的模型比 为0.80的模型拟合的效果好. 为0.80的模型拟合的效果好. |
对变量 有观测数据
有观测数据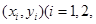 …,10),得散点图(1)所示.对变量
…,10),得散点图(1)所示.对变量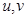 有观测数据
有观测数据 ,…,10),得散点图(2).由这两个散点图可以判断
,…,10),得散点图(2).由这两个散点图可以判断
A.变量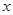 与 与 正相关, 正相关,  与 与 正相关 正相关 |
B.变量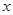 与 与 正相关, 正相关,  与 与 负相关 负相关 |
C.变量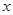 与 与 负相关, 负相关,  与 与 正相关 正相关 |
D.变量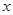 与 与 负相关, 负相关,  与 与 负相关 负相关 |
下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨)标准煤的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程 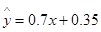 ,那么表中m的值为( )
,那么表中m的值为( )
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
m |
4 |
4.5 |
A. 4 B. 3.5 C. 4.5 D. 3
实验测得四组 的值分别为
的值分别为 ,则y关于x的线性回归方程必过点( )
,则y关于x的线性回归方程必过点( )
| A.(2,8) | B.(2.5,8) |
| C.(10,31) | D.(2.5,7.75) |
在对两个变量x、y进行线性回归分析时一般有下列步骤:
①对所求出的回归方程作出解释;
②收集数据 [
[
③求线性回归方程;
④求相关系数;
⑤根据所搜集的数据绘制散点图.
若根据实际情况能够判定变量x、y具有线性相关性,则在下列操作顺序中正确的是
| A.①②⑤③④ | B.③②④⑤① | C.②④③①⑤ | D.②⑤④③① |
给出以下四个说法:
①在匀速传递的产品生产流水线上,质检员每间隔 分钟抽取一件产品进行某项指标的检测 ,这样的抽样是分层抽样;
分钟抽取一件产品进行某项指标的检测 ,这样的抽样是分层抽样;
②在刻画回归模型的拟合效果时,相关指数 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;
③在回归直线方程 中,当解释变量
中,当解释变量 每增加一个单位时,预报变量
每增加一个单位时,预报变量 平均增加
平均增加 个单位;
个单位;
④对分类变量 与
与 ,若它们的随机变量
,若它们的随机变量 的观测值
的观测值 越小,则判断“
越小,则判断“ 与
与 有关系”的把握程度越大.
有关系”的把握程度越大.
其中正确的说法是
| A.①④ | B.②④ | C.①③ | D.②③ |
设(x1,y1),(x2,y2),…,(xn,yn),是变量x:和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是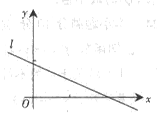
| A. x;和y正相关 |
| B. x和y的相关系数为直线l的斜率 |
| C. x和y的相关系数在-1到0之间 |
| D.当n为偶数时,分布在l两侧的样本点的个数一定相同 |
设(x1,y1),(x2,y2),…,(xn,yn),是变量x:和y的n个样本点,直线Z是由这些样本点通过 最小二乘法得到的线性回归方程(如图),以下结论中正确的是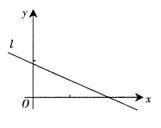
| A.x;和y正相关 |
| B.y和y的相关系数为直线I的斜率 |
| C.x和y的相关系数在-1到O之间 |
| D.当n为偶数时,分布在l两侧的样本点的个数一定相同 |
设有一个线性回归直线方程为 ,则变量
,则变量 每增加一个单位时( )
每增加一个单位时( )
A. 平均增加 1.5 个单位 平均增加 1.5 个单位 |
B. 平均增加 2 个单位 平均增加 2 个单位 |
C. 平均减少 1.5 个单位 平均减少 1.5 个单位 |
D. 平均减少 2 个单位 平均减少 2 个单位 |
试题篮
()