高中数学变量间的相关关系试题

（本小题满分12分）
某公司近年来科研费用支出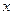万元与公司所获得利润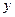万元之间有如下的统计数据：

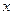	2	3	4	5
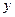	18	27	32	35

(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出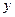关于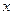的线性回归方程；
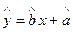(3)试根据(2)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润.
参考公式:

下面的茎叶图是某赛季甲乙两名篮球运动员比赛得分的
情况：

根据茎叶图分析    发挥更稳定

给出下列结论：
（1）在回归分析中，可用指数系数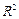的值判断模型的拟合效果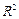，越大，模型的拟合效果越好；
（2）在回归分析中，可用残差平方和判断模型的拟合效果，残差平方和越大，模型的拟合效果越好；
（3）在回归分析中，可用相关系数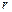的值判断模型的拟合效果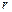，越小，模型的拟合效果越好；
（4）在回归分析中，可用残差图判断模型的拟合效果，残差点比较均匀地落在水平的带状区域中，说明这样的模型比较合适．带状区域的宽度越窄，说明模型的拟合精度越高．
以上结论中，正确的有（   ）个．                  

A．1

B．2

C．3

D．4

某班主任对全班50名学生进行了作业量多少的调查，数据如下表：

	认为作业多	认为作业不多	总数
喜欢玩电脑游戏	18	9	27
不喜欢玩电脑游戏	8	15	23
总数	26	24	50

根据表中数据得到5.059，因为p(K≥5.024)=0.025,
则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为（   ）

A．2.5％

B．95％

C．97.5％

D．不具有相关性

下表是某厂1～4月份用水量（单位：百吨）的一组数据：

月 份x	1	2	3	4
用水量y	4.5	4	3	2.5

由散点图可知，用水量y与月份x之间有较好的线性相关关系，其线性回归直线方程是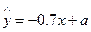，则=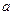

A．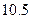

B．

C．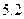

D．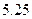

如图是在一次全国少数民族运动会上，七位评委为某民族舞蹈打出的分数的茎叶图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为   

A．84，4.84	B．84,1.6
C．85,1.6	D．85,4

 

回归方程，则（  ）

A．

B．是回归系数

C．是回归系数

D．时，

A，B两名同学在5次数学考试中的成绩统计如下面的茎叶图所示，若A，B两人的平均成绩分别是，观察茎叶图，下列结论正确的是（   ）

A．，B比A成绩稳定

B．，B比A成绩稳定

C．，A比B成绩稳定

D．，A比B成绩稳定

‘

如图是从甲、乙两个班级各随机选出9名同学进行测验成绩的茎叶图，从图中看，平均成绩较高的是   ▲   班．

施化肥量x kg与水稻产量y kg在一定范围内线性相关，若回归直线方程为＝5x+250，当施化肥量为80 kg时，预计水稻的产量为_________．

已知回归直线的斜率的估计值是1.23，样本点的中心为(4，5)，则回归直线的方程是（   ）

A．=1.23x＋4	B．="1.23x+5"
C．="1.23x+0.08"	D．=0.08x+1.23

下列关系中是相关关系的是（   ）

A．位移与速度、时间的关系	B．烧香的次数与成绩的关系
C．广告费支出与销售额的关系	D．物体的加速度与力的关系

在如图所示的“茎叶图”表示的数据中，众数和中位数分别是（  ）
Ａ.23与26　　　　　B.31与26
C.24与30　　       D.26与30　　

 

一组数据中每个数据都减去构成一组新数据，则这组新数据的平均数是，方差是，则原来一组数的方差为（      ）.
 3.2   4.4     4.8      5.6

人的年龄x与人体脂肪含量y的回归方程为如果某人36岁，那么这个人的脂肪含量（     ） 

A．为20.3％

B．在20.3％附近的可能性较大

C．无参考数据

D．以上解释都无道理