某种产品表面进行腐蚀性试验,得到腐蚀深度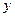 与腐蚀时间
与腐蚀时间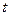 之间对应的一组数据:
之间对应的一组数据:
时间 |
深度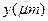 |
| 5 |
6 |
| 10 |
10 |
| 15 |
10 |
| 20 |
13 |
| 30 |
16 |
| 40 |
17 |
| 50 |
19 |
| 60 |
23 |
| 70 |
25 |
| 90 |
29 |
| 120 |
46 |
(1)试求腐蚀深度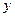 对时间
对时间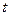 的回归直线方程;
的回归直线方程;
(2)预测腐蚀时间为80 s时产品腐蚀的深度大约是多少?
下表是某省的20个县城2006年的一份统计资料,其中 表示第i个县城在2006年建成的新住宅的面积(单位:万平方米),
表示第i个县城在2006年建成的新住宅的面积(单位:万平方米), 表示第i个县城在2006年的家具销售额(单位:万元)
表示第i个县城在2006年的家具销售额(单位:万元)
| 县城编号 |
xi |
yi |
县城编号 |
xi |
yi |
| 1 |
121 |
360 |
11 |
387 |
602 |
| 2 |
118 |
260 |
12 |
270 |
540 |
| 3 |
271 |
440 |
13 |
218 |
414 |
| 4 |
190 |
400 |
14 |
342 |
590 |
| 5 |
75 |
360 |
15 |
173 |
492 |
| 6 |
263 |
500 |
16 |
370 |
660 |
| 7 |
334 |
580 |
17 |
170 |
360 |
| 8 |
368 |
560 |
18 |
205 |
410 |
| 9 |
305 |
505 |
19 |
339 |
680 |
| 10 |
210 |
480 |
20 |
283 |
594 |
试求 对
对 的回归方程.
的回归方程.
已知10只狗的血球体积及红血球的测量值如下
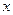 |
 |
| 45 |
6.53 |
| 42 |
6.30 |
| 46 |
9.25 |
| 48 |
7.50 |
| 42 |
6.99 |
| 35 |
5.90 |
| 58 |
9.49 |
| 40 |
6.20 |
| 39 |
6.55 |
| 50 |
7.72 |
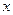 (血球体积,mm),
(血球体积,mm), (红血球数,百万)
(红血球数,百万)
(1) 画出上表的散点图;
(2)求出回归直线并且画出图形;
(3)若血球体积为49mm,预测红血球数大约是多少?
商场对某种产品的广告费用支出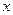 (元)与销售额
(元)与销售额 (元)之间的关系进行调查,通过回归分析,求得
(元)之间的关系进行调查,通过回归分析,求得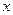 与
与 之间的关系式为
之间的关系式为 ,则当广告费用支出为10元时,销售额
,则当广告费用支出为10元时,销售额 的预报值为
的预报值为
以下是某地区的降雨量(单位:mm)与年平均气温(单位:0C)的一组数据:
根据这组数据可以推测:该地区的降雨量与年平均气温 相关关系(填“具有”或“不具有”)
| 平均 气温 |
12.51 |
12.84 |
12.84 |
13.69 |
13.33 |
12.74 |
13.05 |
| 降雨 量 |
748 |
542 |
507 |
813 |
574 |
701 |
432 |
某考察团对全国10大城市进行职工人均平均工资 与居民人均消费
与居民人均消费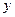 进行统计调查,
进行统计调查, 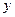 与
与 具有相关关系,回归方程
具有相关关系,回归方程 (单位:千元),若某城市居民消费水平为7.675,估计该城市消费额占人均工资收入的百分比为( )
(单位:千元),若某城市居民消费水平为7.675,估计该城市消费额占人均工资收入的百分比为( )
| A.66% | B.72.3% | C.67.3% | D.83%. |
已知x与y之间的一组数据,则y与x的线性回归方程为y=bx+a必过( )
| x |
0 |
1 |
2 |
3 |
| y |
1 |
3 |
5 |
7 |
A.点 |
B.点 |
C.点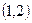 |
D.点 |
对于两个变量之间的相关系数,下列说法中正确的是( )
A. 越大,相关程度越大 越大,相关程度越大 |
B.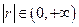 , , 越大,相关程度越小, 越大,相关程度越小, 越小,相关程度越大 越小,相关程度越大 |
C. 且 且 越接近于 越接近于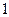 ,相关程度越大; ,相关程度越大; 越接近于 越接近于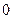 ,相关程度越小 ,相关程度越小 |
| D.以上说法都不对 |
考察棉花种子经过处理跟生病之间的关系得到如下表数据:
| |
种子处理 |
种子未处理 |
合计 |
| 得病 |
32 |
101 |
133 |
| 不得病 |
61 |
213 |
274 |
| 合计 |
93 |
314 |
407 |
根据以上数据,则( ).
| A.种子经过处理跟是否生病有关 | B.种子经过处理跟是否生病无关 |
| C.种子是否经过处理决定是否生病 | D.以上都是错误的 |
把一组数据中的每一个数据都减去80,得一组新数据,若求得新数据的平均数是1.2,
方差是4.4,则原来数据的平均数和方差分别是( )
| A.78.8,75.6 | B.78.8,4.4 |
| C.81.2,84.4 | D.81.2,4.4 |
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
(1)求线性回归方程;
(2)预测当广告费支出7(百万元)时的销售额。
(用最小二乘法求线性回归方程系数公式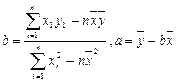 )
)
试题篮
()