科研人员为了全面掌握棉花新品种的生产情况,查看了气象局对该地区年降雨量与年平均气温的统计数据(单位分别是mm,℃),并作了统计.
| 年平均气温 |
12.51 |
12.84 |
12.84 |
13.69 |
13.33 |
12.74 |
13.05 |
| 年降雨量 |
748 |
542 |
507 |
813 |
574 |
701 |
432 |
(1)试画出散点图;
(2)判断两个变量是否具有相关关系.
随着我国经济的快速发展,城乡居民的生活水平不断提高,为研究某市家庭平均收入与月平均生活支出
的关系,该市统计部门随机调查了10个家庭,得数据如下:
| 家庭编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| xi(收入)千元 |
0.8 |
1.1 |
1.3 |
1.5 |
1.5 |
1.8 |
2.0 |
2.2 |
2.4 |
2.8 |
| yi(支出)千元 |
0.7 |
1.0 |
1.2 |
1.0 |
1.3 |
1.5 |
1.3 |
1.7 |
2.0 |
2.5 |
(1)判断家庭平均收入与月平均生活支出是否相关?
(2)若二者线性相关,求回归直线方程.
下面是水稻产量与施化肥量的一组观测数据:
施化肥量 15 20 25 30 35 40 45
水稻产量 320 330 360 410 460 470 480
(1)将上述数据制成散点图;
(2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗?水稻产量会一直随施化肥量的增加而增长吗?
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?
以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
| 房屋面积x(m2) |
115 |
110 |
80 |
135 |
105 |
| 销售价格y(万元) |
24.8 |
21.6 |
18.4 |
29.2 |
22 |
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线.
在研究硝酸钠的可溶性程度时,对于不同的温度观测它在水中的溶解度,得观测结果如下:
| 温度(x) |
0 |
10 |
20 |
50 |
70 |
| 溶解度(y) |
66.7 |
76.0 |
85.0 |
112.3 |
128.0 |
由资料看y与x呈线性相关,试求回归方程.
人的年龄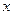 与人体脂肪含量的百分数
与人体脂肪含量的百分数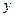 的回归方程为
的回归方程为 ,如果某人
,如果某人 岁,那么这个人的脂肪含量 ( )
岁,那么这个人的脂肪含量 ( )
A.一定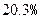 |
B.在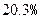 附近的可能性比较大 附近的可能性比较大 |
| C.无任何参考数据 | D.以上解释都无道理 |
有下列关系:(1)人的年龄与其拥有的财富之间的关系;(2)曲线上的点与该点的坐标之间的关系;(3)苹果的产量与气候之间的关系;(4)森林中的同一树木,其横截面直径与高度之间的关系;(5)学生与其学校之间的关系.其中有相关关系的是 .
大学生和研究生毕业的一个随机样本给出了关于所获取学位类别与学生性别的分类数据如下表所示:
| |
硕士 |
博士 |
合计 |
| 男 |
162 |
27 |
189 |
| 女 |
143 |
8 |
151 |
| 合计 |
305 |
35 |
340 |
根据以上数据,则 ( )
| A.性别与获取学位类别有关 | B.性别与获取学位类别无关 |
| C.性别决定获取学位的类别 | D.以上都是错误的 |
(本小题满分12分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗Y(吨标准煤)的几组对照数据
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图; (2)请根据上表提供的数据,用最小二乘法求出Y关于x的线性回归方程Y=bx+a;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:32.5+43+54+64.5=66.5)
试题篮
()