从某居民区随机抽取10个家庭,获得第个家庭的月收入
(单位:千元)与月储蓄
(单位:千元)的数据资料,算得
.(1)求家庭的月储蓄
对月收入
的线性回归方程
;
(2)判断变量与
之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程中,
,其中
为样本平均值,线性回归方程也可写为
.
某产品的广告费用与销售额
的统计数据如下表
| 广告费用 |
4 |
2 |
3 |
5 |
| 销售额 |
49 |
26 |
39 |
54 |
根据上表可得回归方程的
为9.4,据此模型预报广告费用为6万元时销售额为( )
| A. |
63.6万元 |
B. |
65.5万元 |
C. |
67.7万元 |
D. |
72.0万元 |
某单位随机统计了某4天的用电量(度)与当天气温( )如下表,以了解二者的关系。
)如下表,以了解二者的关系。
气温( ) ) |
18 |
13 |
10 |
-1 |
| 用电量(度) |
24 |
34 |
38 |
64 |
由表中数据得回归直线方程 ,则
,则
A.60 B.58 C.40 D.以上都不对
某商店统计了最近6个月某商品的进价x(元)与售价y(元)的对应数据如下表:
| x |
3 |
5 |
2 |
7 |
8 |
11 |
| y |
4 |
6 |
3 |
9 |
12 |
14 |
则回归直线方程是_______________.
注:线性回归直线方程系数公式: 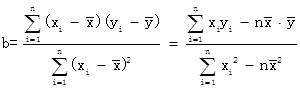 ,a=y-bx
,a=y-bx
一机器可以按各种不同的速度运转,其生产物件有一些会有缺点,每小时生产有缺点物件的多少随机器运转速度而变化,用 表示转速(单位转/秒),用
表示转速(单位转/秒),用 表示每小时生产的有缺点物件个数,现观测得到
表示每小时生产的有缺点物件个数,现观测得到 的4组观测值为(8,5),(12,8),(14,9),(16,11).
的4组观测值为(8,5),(12,8),(14,9),(16,11).
(1)假定 与
与 之间有线性相关关系,求
之间有线性相关关系,求 对
对 的回归直线方程.
的回归直线方程.
(2)若实际生产中所容许的每小时最大有缺点物件数为10,则机器的速度不得超过多少转/秒?(精确到1转/秒)
(参考公式 )
)
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全班50人中随机抽取1人,抽到喜爱打篮球的学生的概率为 .
.
(1)请将上表补充完整(不用写计算过程);
(2)能否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由.下面的临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)
在2014年元旦期间,某市物价部门对本市五个商场销售的某商品一天的销售量及其价格进行调查,五个商场的售价x元和销售量y件之间的一组数据如表所示:
| 价格x |
9 |
9.5 |
10 |
10.5 |
11 |
| 销售量y |
11 |
10 |
8 |
6 |
5 |
通过分析,发现销售量y与商品的价格x具有线性相关关系,则销售量y关于商品的价格x的线性回归方程为__________.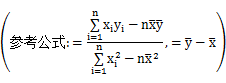
进入4月份,天气渐暖,蔬菜上市品种逐渐增加.某蔬菜销售市场,根据连续5周的市场调研,对某种蔬菜的销售量 (千克)与价格
(千克)与价格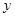 (元∕千克)统计数据(如表所示)表明:二者负相关,其回归方程为
(元∕千克)统计数据(如表所示)表明:二者负相关,其回归方程为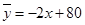 ,则统计表格中的实数
,则统计表格中的实数 的值为( )
的值为( )
| 周次 |
1 |
2 |
3 |
4 |
5 |
销售量 |
18 |
19 |
18 |
22 |
23 |
价格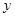 |
45 |
43 |
 |
35 |
33 |
A.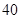 B.
B.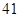 C.
C.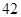 D.
D.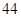
给出下列五个命题:
①某班级一共有52名学生,现将该班学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知7号,33号,46号同学在样本中,那么样本另一位同学的编号为23;
②一组数据1、2、3、3、4、5的平均数、众数、中位数相同;
③一组数据a、0、1、2、3,若该组数据的平均值为1,则样本标准差为2;
④根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为
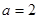 ,
,  ,则
,则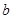 =1;
=1;
⑤如图是根据抽样检测后得出的产品样本净重(单位:克)数据绘制的频率分布直方图,已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克,并且小于104克的产品的个数是90.
其中真命题为: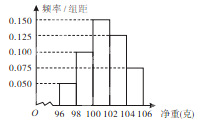
| A.①②④ | B.②④⑤ | C.②③④ | D.③④⑤ |
某种产品的广告费支出x与销售额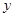 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
50 |
60 |
70 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 .
.
(3)经计算,相关指数 ,你可得到什么结论?
,你可得到什么结论?
(参考数值:2×30+4×40+5×50+6×60+8×70==1390)
已知 与
与 之间的几组数据如下表:
之间的几组数据如下表:
 |
1 |
2 |
3 |
4 |
5 |
6 |
 |
0 |
2 |
1 |
3 |
3 |
4 |
假设根据上表数据所得线性回归直线方程为 .若某同学根据上表中前两组数据
.若某同学根据上表中前两组数据 和
和 求得的直线方程为
求得的直线方程为 ,则以下结论正确的是( )。
,则以下结论正确的是( )。
A. B.
B. C.
C. D.
D.
下表提供了某厂节能降耗技术改造后在生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗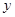 (吨)的几组对应数据:
(吨)的几组对应数据:
 |
3 |
4 |
5 |
6 |
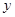 |
2.5 |
3 |
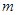 |
4.5 |
若根据上表提供的数据用最小二乘法可求得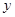 对
对 的回归直线方程是
的回归直线方程是 0.7
0.7 +0.35,则表中
+0.35,则表中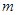 的值为( )
的值为( )
A.4 B.4.5 C.3 D.3.5
观察下列关于变量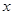 和
和 的三个散点图,它们从左到右的对应关系依次是( )
的三个散点图,它们从左到右的对应关系依次是( )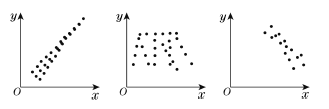
| A.正相关、负相关、不相关 | B.负相关、不相关、正相关 |
| C.负相关、正相关、不相关 | D.正相关、不相关、负相关 |
观察下列关于两个变量 和
和 的三个散点图,它们从左到右的对应关系依次为( )
的三个散点图,它们从左到右的对应关系依次为( )
| A.正相关、负相关、不相关 | B.负相关、不相关、正相关 |
| C.负相关、正相关、不相关 | D.正相关、不相关、负相关 |
试题篮
()