高中数学变量间的相关关系试题

已知回归直线的斜率的估计值为1．23，样本点的中心为（4，5），则回归直线方程为（   ）

A．	B．
C．	D．

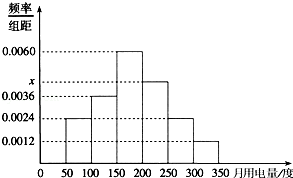
从某小区抽取100户居民进行月用电量调查，发现其用电量都在50至350度之间，频率分布直方图如图所示：
（1）直方图中 $x$的值为；
（2）在这些用户中，用电量落在区间 $[100,250)$内的户数为．

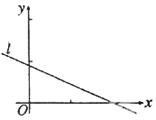
设是变量和的个样本点，直线是由这些样本点通过最小二乘法得到的线性回归方程（如图），以下结论中正确的是（ ）

A．	和 的相关系数为直线 的斜率
B．	和 的相关系数在0到1之间
C．	当 为偶数时，分布在 两侧的样本点的个数一定相同
D．	直线 过点

已知下列表格所示的数据的回归直线方程为多，则a的值为          ．

已知x，y取值如下表：

x	0	1	4	5	6	8
y	1．3	1．8	5．6	6．1	7．4	9．3

 
从所得的散点图分析可知：y与x线性相关，且＝0．95x＋a，则a＝________．

下表是某旅游区游客数量与平均气温的对比表：

平均气温(℃)	－1	4	10	13	18	26
数量(百个)	20	24	34	38	50	64

 
若已知游客数量与平均气温是线性相关的，则回归方程为（   ）．
A.＝1.98x＋22.13
B.＝1.78x＋20.13
C.＝1.68x＋18.73
D.＝1.51x＋15.73

实验测得四组(x，y)的值为(1,2)，(2,3)，(3,4)，(4,5)，则y与x之间的回归直线方程为(    )

A．＝x＋1	B．＝x＋2
C．＝2x＋1	D．＝2x＋2

一般来说，一个人脚越长，他的身高就越高．现对10名成年人的脚长x(单位：cm)与身高y(单位：cm)进行测量，得如下数据：

x	20	21	22	23	24	25	26	27	28	29
y	141	146	154	160	169	176	181	188	197	203

作出散点图后，发现散点在一条直线附近．
经计算得到一些数据：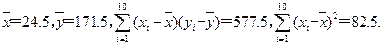
某刑侦人员在某案发现场发现一对裸脚印，量得每个脚印长26.5 cm，请你估计案发嫌疑人的身高为(    )
A.185       B.185.5         C.186         D.186.5

下列命题：
①任何两个变量都具有相关关系；②圆的周长与该圆的半径具有相关关系；③某商品的需求量与该商品的价格是一种非确定性关系；④根据散点图求得的回归直线方程可能是没有意义的；⑤两个变量间的相关关系可以通过回归直线，把非确定性问题转化为确定性问题进行研究．其中正确的命题个数为(    )

A．2

B．3

C．4

D．5

为研究变量和的线性相关性，甲、乙二人分别作了研究，利用线性回归方法得到回归直线方程和，两人计算知相同，也相同，下列正确的是（     ）

A．与重合	B．与一定平行
C．与相交于点	D．无法判断和是否相交

某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数．

（1）若日加工零件个数大于样本均值的工人为优秀工人，根据茎叶图推断该车间12名工人中有几名优秀工人？
（2）从这6名工人中任取2人，设这两人加工零件的个数分别为，求的概率．

对某项活动中800名青年志愿者的年龄抽样调查后，得到如下图所示的频率分布直方图，但年龄在（25,30)的数据不慎丢失．

依据此图，估计该项活动中年龄在（25,30)的志愿者人数为________．

已知回归直线的斜率的估计值是1．23，样本点的中心为(4,5)，则回归直线的方程是(　)

A．	B．
C．	D．

某学生课外活动兴趣小组对两个相关变量收集到5组数据如下表：

x	10	20	30	40	50
y	62	■	75	81	89

由最小二乘法求得回归方程为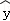=0.67x+54.9，现发现表中有一个数据模糊不清，请推断该点数据的值为（　　）
A．67        B．68        C．69        D．70

如图是根据变量x，y的观测数据（x_i，y_i）（i=1，2，…10）得到的散点图，由这些散点图可以判断变量x，y具有相关关系的图是（　　）

A．①②

B．①④

C．②③

D．③④