设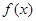 是定义在正整数集上的函数且满足当
是定义在正整数集上的函数且满足当 成立时,总可以推出
成立时,总可以推出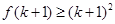 成立,则下列命题总成立的是( )
成立,则下列命题总成立的是( )
A.若 成立 成立 |
B.若 成立,则 成立,则 成立 成立 |
C.若 成立,则当 成立,则当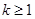 时,均有 时,均有 成立 成立 |
D.若 成立,则当 成立,则当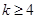 时,均有 时,均有 成立 成立 |
平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:
充要条件① ;
充要条件② .
(写出你认为正确的两个充要条件)
《论语》云:“名不正,则言不顺;言不顺,则事不成;事不成,则礼乐不兴;礼乐不兴,则刑罚不中;刑罚不中,则民无所措手足;所以名不正,则民无所措手足。”上述理由用的是( )
| A.合情推理 | B.归纳推理 | C.类比推理 | D.演绎推理 |
“三角形的三条中线交于一点,且这一点到顶点的距离等于它到对边中点距离的2倍”。试类比:四面体的四条中线(顶点到对面三角形重心的连线段)交于一点,且这一点到顶点的距离等于它到对面重心距离的 倍。
给出下列类比推理:
①已知 ,若
,若 ,则
,则 ,类比得已知
,类比得已知 ,若
,若 ,则
,则 ;
;
②已知 ,若
,若 ,则
,则 类比得已知
类比得已知 ,若
,若 ,则
,则 ;
;
③由实数绝对值的性质 类比得复数
类比得复数 的性质
的性质 ;
;
④已知 ,若复数
,若复数 ,则
,则 ,类比得已知
,类比得已知 ,若
,若 ,则
,则 .
.
其中推理结论正确的是 .
下面几种推理是合情推理的是
(1)由圆的性质类比出球的有关性质;
(2)由直角三角形、等腰三角形、等边三角形内角和是 ,归纳出所有三角形的内角和都是
,归纳出所有三角形的内角和都是 ;
;
(3)某次考试张军成绩是100分,由此推出全班同学成绩都是100分;
(4)三角形内角和是 ,四边形内角和是
,四边形内角和是 ,五边形内角和是
,五边形内角和是 ,由此得凸多边形内角和是
,由此得凸多边形内角和是
| A.(1)(2) | B.(1)(3) | C.(1)(2)(4) | D.(2)(4) |
一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○○●…若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前120个圈中的●的个数是 .
试题篮
()