对于平面几何中的命题:“夹在两条平行线之间的平行线段相等”,在立体几何中,类比上述命题,可以得到命题:“___________________________”这个类比命题的真假性是________
黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案;则第n个图案中有白色地面砖为 块.
 |
已知结论:“在正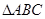 中,
中,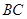 中点为
中点为 ,若
,若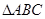 内一点
内一点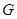 到各边的距离都相等,则
到各边的距离都相等,则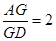 ”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体
”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体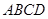 中,若
中,若 的中心为
的中心为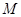 ,四面体内部一点
,四面体内部一点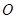 到四面体各面的距离都相等,则
到四面体各面的距离都相等,则 ( ▲ )
( ▲ )
| A.1 | B.2 | C.3 | D.4 |
下列推理是归纳推理的是( )
| A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,得P的轨迹为椭圆 |
| B.由a1=1,an=3n-1(n>1),求出S1,S2,S3,猜想数列的前n项和Sn的表达式 |
C.由圆x2+y2=r2的面积πr2,猜出椭圆 + + =1的面积S=πab =1的面积S=πab |
| D.科学家利用鱼的沉浮原理制造潜艇 |
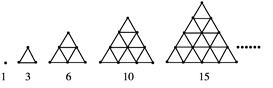
如图,把1,3,6,10,15,…这些数叫做三角形数,这是因为这些数目的点可以排成一个正三角形,则第七个三角形数是
| A.27 | B.28 | C.29 | D.30 |
观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
……
照此规律,第n个等式为
_______________________________.
有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线 平面
平面 ,直线
,直线 平面
平面 ,直线
,直线 ∥平面
∥平面 ,则直线
,则直线 ∥直线
∥直线 ”的结论显然是错误的,这是因为( )
”的结论显然是错误的,这是因为( )
| A.推理形式错误 | B.小前提错误 | C.大前提错误 | D.非以上错误 |
“自然数是整数,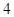 是自然数,所以
是自然数,所以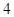 是整数.”以上三段推理( )。
是整数.”以上三段推理( )。
| A.完全正确 |
| B.推理形式不正确 |
| C.不正确,因为两个“自然数”概念不一致 |
| D.不正确,因为两个“整数”概念不一致 |
下列表述正确的是( ).
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理.
| A.①②③; | B.②③④; | C.②④⑤; | D.①③⑤. |
试题篮
()