已知x∈R+,有不等式:x+ ≥2
≥2 =2,x+
=2,x+ =
= +
+ +
+ ≥3
≥3 =3,….启发我们可能推广结论为:x+
=3,….启发我们可能推广结论为:x+ ≥n+1(n∈N*),则a的值为 ( )
≥n+1(n∈N*),则a的值为 ( )
| A.2n | B.nn | C.n2 | D.2n+1 |
设△ 的三边长分别为
的三边长分别为 △
△ 的面积为
的面积为 ,内切圆半径为
,内切圆半径为 ,则
,则 .类比这个结论可知:四面体
.类比这个结论可知:四面体 的四个面的面积分别为
的四个面的面积分别为


 内切球的半径为
内切球的半径为 ,四面体
,四面体 的体积为
的体积为 ,则
,则 =( )
=( )
A. |
B. |
C. |
D. |
设△ 的三边长分别为
的三边长分别为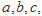 △
△ 的面积为
的面积为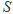 ,内切圆半径为
,内切圆半径为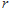 ,则
,则 .类比这个结论可知:四面体
.类比这个结论可知:四面体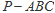 的四个面的面积分别为
的四个面的面积分别为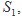
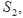

 内切球的半径为
内切球的半径为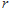 ,四面体
,四面体 的体积为
的体积为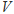 ,则
,则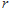 =( )
=( )
A.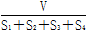 |
B.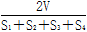 |
C.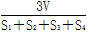 |
D.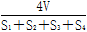 |
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第 行有
行有 个数且两端的数均为
个数且两端的数均为
 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如 ,
, ,
, ,…,则第10行第4个数(从左往右数)为 .
,…,则第10行第4个数(从左往右数)为 .

如图所示为各项均为正数的数列 所排成的三角形数阵,
所排成的三角形数阵, 表示数阵中第
表示数阵中第 行、第
行、第 列的数.已知
列的数.已知 为等比数列,且从第
为等比数列,且从第 行开始,各行均构成公差为
行开始,各行均构成公差为 的等差数列(第
的等差数列(第 行的
行的 个数构成公差为
个数构成公差为 的等差数列;第
的等差数列;第 行的
行的 个数构成公差为
个数构成公差为 的等差数列……).且有
的等差数列……).且有 .
.
(1)数阵第
 行第
行第 列的数
列的数 .
.
(2) 这
这 个数中有 个在数阵中.
个数中有 个在数阵中.
设 ,
, ,
, ,
, 均是实数,下面使用类比推理,得出正确结论的是( )
均是实数,下面使用类比推理,得出正确结论的是( )
A.“若 ,则 ,则 ”类推出“若 ”类推出“若 ,则 ,则 ” ” |
B.“ ”类推出“ ”类推出“ ” ” |
C.“ ”类推出“ ”类推出“ ” ” |
D.“ ”类推出“ ”类推出“ ( ( )” )” |
下面几种推理过程是演绎推理的是( )
A.两条直线平行,同旁内角互补,如果 和 和 是两条平行直线的同旁内角,则 是两条平行直线的同旁内角,则 + + = = |
| B.由平面三角形的性质,推测空间四面体的性质 |
| C.某校高三共有10个班,1班有51人,2班有53人,三班有52人,由此推测各班都超过50人 |
D.在数列 中, 中, , , ,计算 ,计算 ,由此推测通项 ,由此推测通项 |
二维空间中圆的一维测度(周长)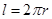 ,二维测度(面积)
,二维测度(面积)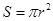 ,观察发现
,观察发现 ;三维空间中球的二维测度(表面积)
;三维空间中球的二维测度(表面积) ,三维测度(体积)
,三维测度(体积)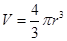 ,观察发现
,观察发现 .则四维空间中“超球”的三维测度
.则四维空间中“超球”的三维测度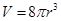 ,猜想其四维测度W= .
,猜想其四维测度W= .
如图所示,在三棱锥S﹣ABC中,SA⊥SB,SB⊥SC,SC⊥SA,且SA,SB,SC和底面ABC所成的角分别为α1,α2,α3,△SBC,△SAC,△SAB的面积分别为S1,S2,S3,类比三角形中的正弦定理,给出空间图形的一个猜想是 .

(本小题满分12分)观察下列等式
 第一个式子
第一个式子
 第二个式子
第二个式子
 第三个式子
第三个式子
 第四个式子
第四个式子
照此规律下去
(Ⅰ)写出第5个等式;
(Ⅱ)你能做出什么一般性的猜想?请用数学归纳法证明猜想.
试题篮
()