高中数学合情推理和演绎推理填空题

已知，，，，，由此可猜想____________

(优选法与试验设计初步)某试验对象取值范围是内的整数，采用分数法确定试点值，则第一个试点值可以是     ．

用火柴棒按下图的方法搭三角形：

按图示的规律搭下去，则所用火柴棒数与所搭三角形的个数之间的关系式可以是         　.

将全体正奇数排成一个三角形数阵：
1
3   5
7   9   11
13  15  17  19
……
按照以上排列的规律，第n 行（n ≥3）从左向右的第3个数为        ．

在平面上，若两个正三角形的边长之比为，则它们的面积之比为；类似地，在空间内，若两个正四面体的棱长之比为，则它们的体积之比为；

有下列各式：
，

……
则按此规律可猜想此类不等式的一般形式为：__ _______________________．

将全体正整数排成一个三角形数阵：
1
2 3
4 5 6
7 8 9 10
. . . . .
按照以上排列的规律，第n行（）从左向右的第3个数为       

德国数学家莱布尼兹发现了下面的单位分数三角形（单位分数是指分子为，分母为正整数的分数），称为莱布尼兹三角形：
根据前5行的规律，写出第6行的数依次是　　　　　　　　　　　

古希腊著名的毕达哥拉斯学派把，这样的数称为“三角形数”，而把1，4，9，这样的数称为“正方形数”.如图可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和，下列等式中，符合这一规律的表达式为      （填序号）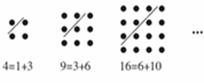

①13=3+10；                  ②25=9+16；
③36=15+21；               ④49=18+31；
⑤64="28+36"

从中得出的一般性结论是_____________.

给出下列不等式：，，…，则按此规律可猜想第n个不等式为      。

已知.观察以上等式，若（，均为正实数），则       .

设ΔABC的三边长分别为a、b、c，ΔABC的面积为S，内切圆半径为r，则r＝；类比这个结论可知：四面体P－ABC的四个面的面积分别为S₁、S₂、S₃、S₄，内切球的半径为R，四面体P－ABC的体积为V，则R＝     

A．

B．

C．

D．

给出下列等式：；         ；
，……
由以上等式推出一个一般结论：
对于=                

调酒师为了调制一种鸡尾酒.每100kg烈性酒中需要加入柠檬汁的量为1000g到2000g之间，现准备用黄金分割法找到它的最优加入量. 如果加入柠檬汁误差不超出1g，需要        次试验.
()