已知命题:在平面直角坐标系xOy中,椭圆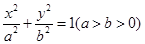 ,△ABC的顶点B在椭圆上,顶点A,C分别为椭圆的左、右焦点,椭圆的离心率为e,则
,△ABC的顶点B在椭圆上,顶点A,C分别为椭圆的左、右焦点,椭圆的离心率为e,则 ,现将该命题类比到双曲线中,△ABC的顶点B在双曲线上,顶点A、C分别为双曲线的左、右焦点,设双曲线的方程为
,现将该命题类比到双曲线中,△ABC的顶点B在双曲线上,顶点A、C分别为双曲线的左、右焦点,设双曲线的方程为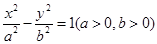 .双曲线的离心率为e,则有________.
.双曲线的离心率为e,则有________.
已知正三角形内切圆的半径是其高的 ,把这个结论推广到空间正四面体,类似的结论是______________________________________.
,把这个结论推广到空间正四面体,类似的结论是______________________________________.
二维空间中圆的一维测度(周长) ,二维测度(面积)
,二维测度(面积) ,观察发现
,观察发现 ;三维空间中球的二维测度(表面积)
;三维空间中球的二维测度(表面积) ,三维测度(体积)
,三维测度(体积) ,观察发现
,观察发现 .则四维空间中“超球”的三维测度
.则四维空间中“超球”的三维测度 ,猜想其四维测度W= .
,猜想其四维测度W= .
如下图所示将若干个点摆成三角形图案,每条边(包括两个端点)有n(n>l,n∈N*)个点,相应
的图案中总的点数记为 ,则
,则 =( )
=( )

A. |
B. |
C. |
D. |
某种平面分形图如下图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为 ; 二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来
; 二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来 的线段,且这两条线段与原线段两两夹角为
的线段,且这两条线段与原线段两两夹角为 ;……;依此规律得到
;……;依此规律得到 级分形图.
级分形图.

(1)4级分形图中共有______条线段;
(2) 级分形图中所有线段长度之和为 .
级分形图中所有线段长度之和为 .
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第 行有
行有 个数且两端的数均为
个数且两端的数均为
 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如 ,
, ,
, ,
, ,则第7行第4个数(从左往右数)为( )
,则第7行第4个数(从左往右数)为( )

A. |
B. |
C. |
D. |
设 是由任意
是由任意 个人组成的集合,如果
个人组成的集合,如果 中任意4个人当中都至少有1个人认识
中任意4个人当中都至少有1个人认识
其余3个人,那么,下面的判断中正确的是 ( )
A. 中没有人认识 中没有人认识 中所有的人 中所有的人 |
B. 中至多有2人认识 中至多有2人认识 中所有的人 中所有的人 |
C. 中至多有2人不认识 中至多有2人不认识 中所有的人 中所有的人 |
D. 中至少有1人认识 中至少有1人认识 中的所有人 中的所有人 |
试题篮
()