高中数学空间向量的应用试题

如图，底面是矩形的四棱锥P—ABCD中AB=2，BC=，侧面PAB是等边三角形，且侧面PAB⊥底面ABCD.
（1）证明：侧面PAB⊥侧面PBC；

（2）求侧棱PC与底面ABCD所成的角；

（3）求直线AB与平面PCD的距离．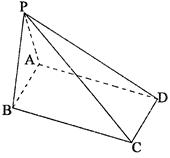

给定下列四个命题的表述：
①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；
②若一个平面经过另一个平面的一条垂线，那么这两个平面相互垂直；  
③垂直于同一直线的两条直线相互平行；．          
④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．
其中，表述正确的命题的是  （      ）

A．②和③

B．①和②

C．②和④

D．③和④

设是两条直线，是两个平面，则的一个充分条件是（   ）

A．	B．
C．	D．

已知，是两个不同的平面，m ，n 是两条不同的直线，则下列正确的是

A．若m //,=" n" ,则m //n

B．若m⊥,n,m ⊥n ,则⊥ 

C．若//,m⊥，n //,则m⊥n

D．若⊥，=" m" ，m //n，则n //

已知菱形ABCD中，AB=4， （如图1所示），将菱形ABCD沿对角线翻折，使点翻折到点的位置（如图2所示），点E，F，M分别是AB，DC₁，BC₁的中点．
（Ⅰ）证明：BD //平面；
（Ⅱ）证明：；
（Ⅲ）当时，求线段AC₁的长．
   

设a，b，c是空间三条直线，，是空间两个平面，则下列命题中，逆命题不成立的是（   ）

A．当c⊥时，若c⊥，则∥

B．当时，若b⊥，则

C．当，且c是a在内的射影时，若b⊥c，则a⊥b

D．当，且时，若c∥，则b∥c

已知两条直线，有以下几个命题，其中是真命题的序号为      。（1）若 （2）
（3） （4）

关于直线以及平面M、N，下面命题中正确的是（   ）

A．若	B．若
C．若	D．若，则

若m、n是互不重合的直线，是互不重合的平面，给出下列命题：（  ）
①若;
②若;
③若m不垂直于内的无数条直线;
④若.
其中正确命题的序号是       

A．①②

B．③④

C．②③

D．②④

已知直线，，则直线的关系是

A．平行

B．相交

C．异面

D．以上都有可能

如图所示，四棱锥P-ABCD的底面ABCD是边长为1的菱形，∠BCD＝60°，E是CD的中点，PA⊥底面ABCD，PA＝2.
（Ⅰ）证明：平面PBE⊥平面PAB;
（Ⅱ）求平面PAD和平面PBE所成二面角（锐角）的大小.

在空间中，a,b是不重合的直线，是不重合的平面，则下列条件中可推出a∥b的是(   )

A．?	B．
C．?	D．

设为三条不同的直线，为两个不同的平面，下列命题中正确的是（ ）

A．若则

B．若则

C．若则

D．若则

下列条件中，能使的条件是（   ）

A．平面内有无数条直线平行于平面

B．平面与平面同平行于一条直线

C．平面内有两条直线平行于平面

D．平面内有两条相交直线平行于平面

四棱锥中，侧面⊥底面，底面是边长为的正方形，又，，分别是的中点．
（Ⅰ）求证：；
（Ⅱ）求二面角的余弦值．