(本小题满分14分)如图,在三棱锥P- ABC中,已知平面PBC  平面ABC.
平面ABC.
(1)若AB BC,CP
BC,CP PB,求证:CP
PB,求证:CP PA:
PA:
(2)若过点A作直线 ⊥平面ABC,求证:
⊥平面ABC,求证: //平面PBC.
//平面PBC.
有一根旗杆 高
高 ,它的顶端
,它的顶端 挂一条长
挂一条长 的绳子,拉紧绳子并把它的下端放在地面上的两点(和旗杆脚不在同一直线上)
的绳子,拉紧绳子并把它的下端放在地面上的两点(和旗杆脚不在同一直线上) ,如果这两点都和旗杆脚
,如果这两点都和旗杆脚 的距离是
的距离是 ,那么旗杆就和地面垂直,为什么?
,那么旗杆就和地面垂直,为什么?
如图,三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,DE垂直平分线段PC,且分别交AC、PC于D、E两点,又PB=BC,PA=AB。
(1)求证:PC⊥平面BDE;
(2)若点Q是线段PA上任一点,判断BD、DQ的位置关系,并证明你的结论;
(3)若AB=2,求三棱锥B-CED的体积
(本小题满分12分)如图,过四棱柱 形木块上底面内的一点
形木块上底面内的一点 和下底面的对角线
和下底面的对角线 将木块锯开,得到截面
将木块锯开,得到截面 .
.
(1)请在木块的上表面作出过 的锯线
的锯线 ,并说明理由;
,并说明理由;
(2)若该四棱柱的底面为菱形,四边形时矩形 ,试证明:平面
,试证明:平面 平面
平面 .
.
如图:C、D是以AB为直径的圆上两点, 在线段
在线段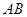 上,且
上,且 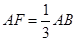 ,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上.
,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上.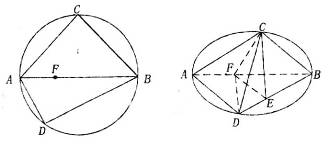
(I)求证平面ACD⊥平面BCD;
(II)求证:AD//平面CEF.
(本小题满分14分)如图,在五面体 中,四边形
中,四边形 为正方形,
为正方形, ,平面
,平面
 平面
平面 ,且
,且 ,
, ,点G是EF的中点.
,点G是EF的中点.
(Ⅰ)证明:

 ;
;
(Ⅱ)若点 在线段
在线段 上,且
上,且 ,求证:
,求证: //平面
//平面 ;
;
(Ⅲ)已知空间中有一点O到 五点的距离相等,请指出点
五点的距离相等,请指出点 的位置. (只需写出结论)
的位置. (只需写出结论)
(本小题满分14分)
如图,四边形 是正方形,△
是正方形,△ 与△
与△ 均是以
均是以 为直角顶点的等腰直角三角形,点
为直角顶点的等腰直角三角形,点 是
是 的中点,点
的中点,点 是边
是边 上的任意一点.
上的任意一点.
(1)求证: ;
;
(2)求二面角 的平面角的正弦值.
的平面角的正弦值.
如图已知:菱形 所在平面与直角梯形
所在平面与直角梯形 所在平面互相垂直,
所在平面互相垂直, ,
, 点
点 分别是线段
分别是线段 的中点.
的中点. 
(1)求证:平面
 平面
平面 ;
;
(2)点 在直线
在直线 上,且
上,且 //平面
//平面 ,求平面
,求平面 与平面
与平面 所成角的余弦值。
所成角的余弦值。
试题篮
()